Предмет: Алгебра,
автор: вкпа
15 БАЛЛОВ. найти предел функции
Приложения:
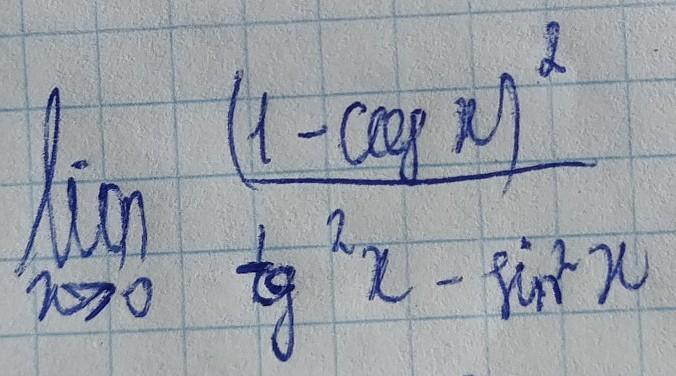
Ответы
Автор ответа:
1
Автор ответа:
1
Ответ
и решение во вложении
Приложения:

Похожие вопросы
Предмет: Математика,
автор: agilyaadilbekkyzy65
Предмет: Математика,
автор: jatskanichvika
Предмет: Математика,
автор: ShlyaM4ik
Предмет: Биология,
автор: Бурджон
Предмет: Химия,
автор: 777778993846382