Question

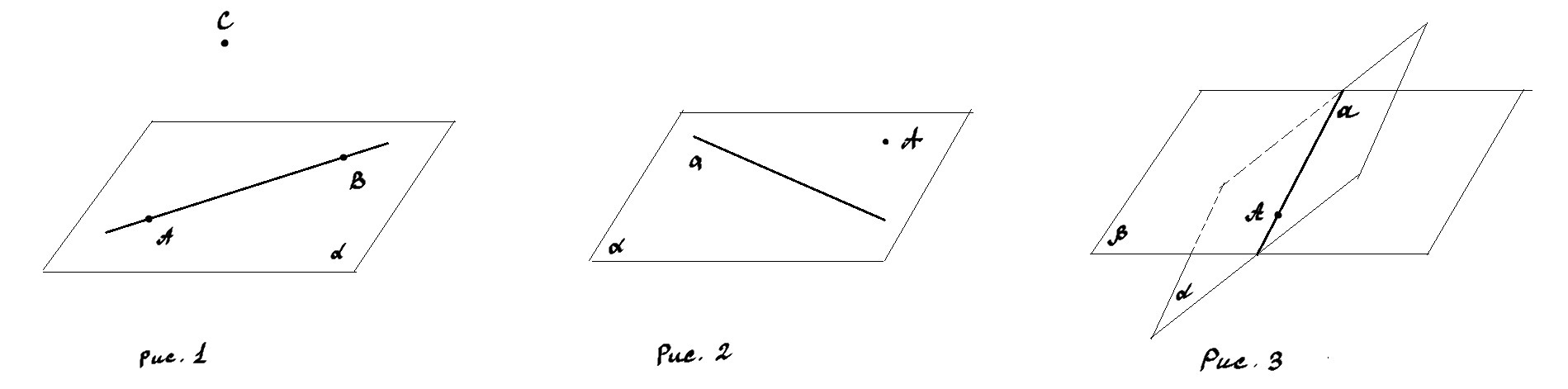
1.Точки А и В принадлежат плоскости a(альфа),а точка С лежит вне плоскости а. Выберите правильное утверждение:
А.Прямая АС лежит в плоскости а
Б.Прямая АВ леит вне плоскости а.
В.Прямая АВ лежит в плоскости а
Г.Прямая СВ лежит в плоскости а
2.В пространстве дана произвольная прямая а и точка А.Отметьте ,какие из следующих четырех утверждений правильные,а какие не.
А.Через прямую а и точку А всегда можно провести плоскость.
Б.Если плоскость проходит через прямую а,то она обязательно содержит точку А.
В. если через прямую а и точку А можно провести только одну плоскость ,то прямая а проходит через точку А
Г. Если через прямую а и точку А можно провести две разные плоскости ,то точка А лежит на прямой а

Answer 1

1. Верно утверждение под буквой В: прямая АВ лежит в плоскости α.

Точки А и В принадлежат плоскости α, значит все точки прямой АВ принадлежат плоскости α (смотри рис.1).

2. Верны утверждения под буквами А и Г.

А: через прямую а и точку А всегда можно провести плоскость.

Если точка А не лежит на прямой а, то можно провести только одну плоскость (см. рис. 2). Если точка А принадлежит прямой а, то плоскостей можно провести бесконечное множество (рис. 3). В любом случае плоскость можно провести.

Г: если через прямую а и точку А можно провести две разные плоскости, то точка А лежит на прямой а.

Если бы точка А не принадлежала прямой а, то через эту точку и прямую можно было бы провести только одну плоскость (см. рис. 2).

Поскольку плоскостей можно провести две, то точка А принадлежит прямой а. В этом случае можно провести бесконечное множество плоскостей (см. рис. 3).