Question

В равнобедренном треугольнике АВС АС=АВ, AD=AE, М - точка пересечения CD и BЕ. Доказать, что АО перпендикулярна ВС.

Answer 1

Ответ:

1) АВ = АС, AD = AE, ∠DAE – общий для ΔBAE и ΔCAD  => ΔBAE  = ΔCAD (по 1-ому признаку равенства Δ-ов)

=> ∠ABE = ∠ACD, ∠AEB = ∠ADC

 

2) ∠CEB = 180° - ∠AEB, ∠BDC = 180° – ∠ADC => ∠CEB = ∠BDC  

3) АВ = АС, AD = AE, CE = AC - AE, BD = AB - AD => CE = BD  

4) CE = BD, ∠CEM = ∠BDM, ∠ECM = ∠DBM => ΔCEM = ΔBDM (по 2-ому признаку равенства Δ-ов)

=> DM = EM, BM = CM  

5) DM = EM, AE = AD, ∠ADM = ∠AEM => ΔAEM = ΔADM (по 1-ому признакуравенства Δ-ов)

=> ∠AMD = ∠AME

 6) ∠AMD = ∠CMO, ∠AME = ∠BMO (т.к. вертикальные углы) => ∠CMO = ∠BMO  

7) BM = CM, ∠CMO = ∠BMO, MO – общая для ΔCMO и ΔBMO => ΔCMO = ΔBMO (по 1-ому признаку равенства Δ-ов)

=> BO = CO => AO – медиана ΔABC => AO – высота ΔABC (т.к. ΔABC – равнобедренный) => AO ⊥ BC

Объяснение:

Answer 2

ΔDBC = ΔECB по двум сторонам и углу между ними:

• АВ = АС , АD = AE  ⇒  BD = CE

• ВС - общая сторона
• ∠DBC = ∠ECB - как углы при основании равноб-го треугольника

Значит, ВЕ = СD.  Можно заметить, что точки D и Е равноудалены от стороны ВС (в равных треугольниках равные высоты)  ⇒  DE || BC

Следовательно, DECB - равнобедренная трапеция

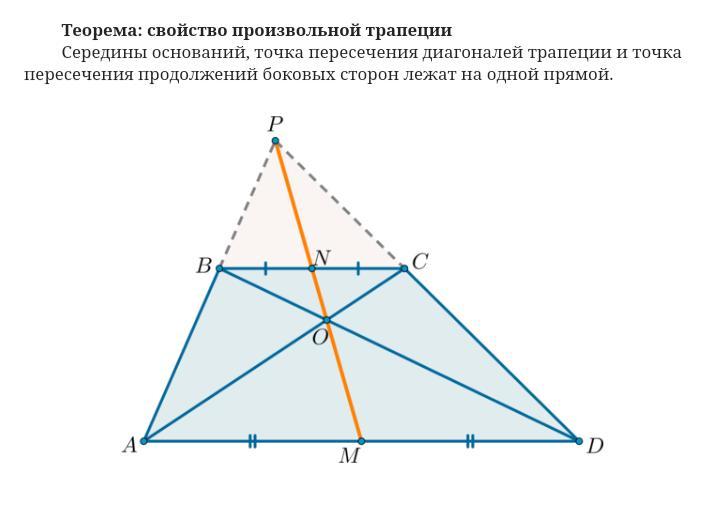
По замечательному свойству трапеции (см. приложение) АО проходит через середины DE и ВС трапеции, поэтому АО⊥ВС, ч.т.д.