Предмет: Математика,
автор: katy770
ДАЮ 40 БАЛЛОВ
найти производную
Приложения:
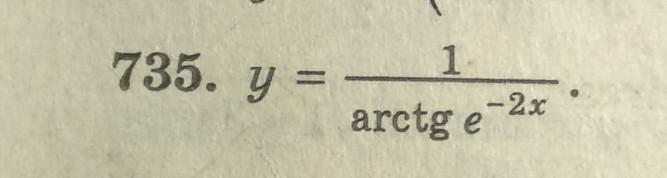
Ответы
Автор ответа:
0
Ответ: решение смотри на фотографии
Пошаговое объяснение:
Приложения:
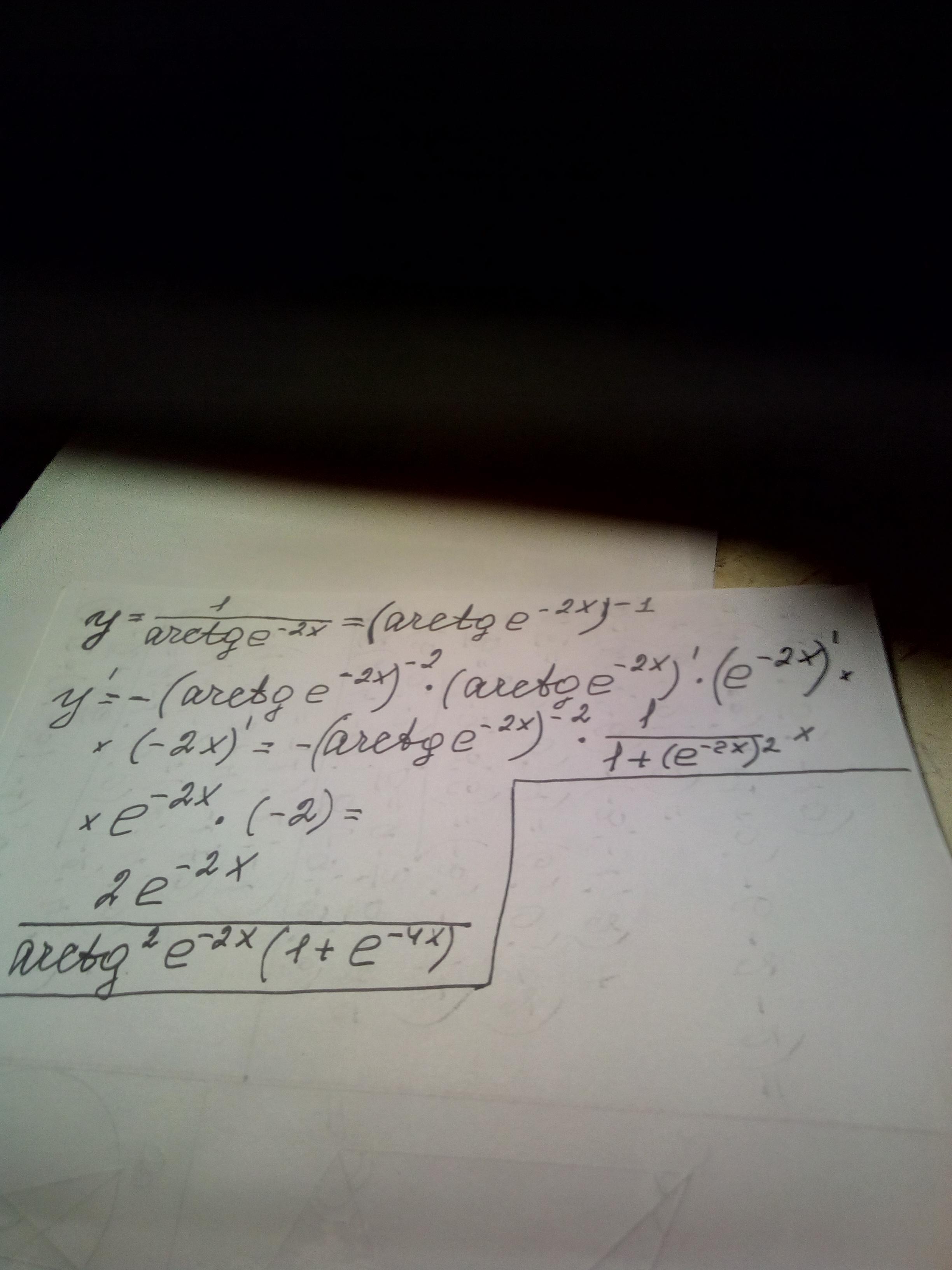
Автор ответа:
1
Это сложная функция.
Производная сложной функции:
Внимательно смотрим на первую формулу. При взятии производной от сложной функции сначала производная берется по "внешней" функции, то есть той, которая вычисляется последней. И вот все то добро, которое у неё в аргументе, никуда не девается.
Формулу можно так записать, чтоб понятнее было:
Запишем нашу функцию через степень.
Тут даже ещё дальше вложенность функций пошла:
И так можно для любого уровня вложенности.
Вспоминаем необходимые нам производные:
Теперь вычисляем наконец:
Чуть-чуть причешем ответ:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: kydyraliyevmaksat71
Предмет: Немецкий язык,
автор: kirritooooo
Предмет: Английский язык,
автор: solijnik891
Предмет: История,
автор: sofa6717
Предмет: Математика,
автор: елена19852