Предмет: Математика,
автор: Damboldorn
Все на фото, интересно кто вообще сможет решить?
Приложения:
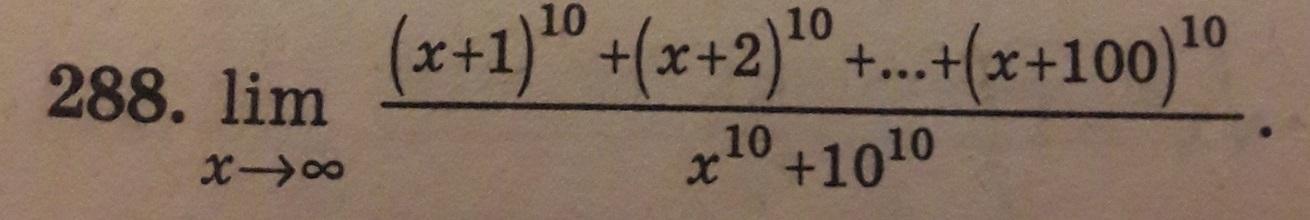
Ответы
Автор ответа:
0
1) Используя бином Ньютона, возведем в 10-ую степень первое слагаемое числителя:
(x+1)¹⁰=х¹⁰+10х⁹+45x⁸+120x⁷+210x⁶+25x⁵+210x⁴+120x³+45x²+10x+1
У данного разложения старшая степень х¹⁰ имеет коэффициент, равный 1.
Аналогично можно возводить в 10-ую степень и остальные слагаемые. НО делать этого не нужно, т.к. очевидно, что у каждого слагаемого при разложении старшая степень х¹⁰ имеет коэффициент равный 1.
2) Всего в числителе 100 слагаемых, таким образом получаем сумму старших степеней с коэффициентом, равным 100.
х¹⁰+х¹⁰+...+х¹⁰ = 100х¹⁰
3) Теперь возвратимся к данному пределу, оставив только старшие степени числителя и знаменателя:
Похожие вопросы
Предмет: Литература,
автор: relisaveta
Предмет: Қазақ тiлi,
автор: Simvababababa
Предмет: Математика,
автор: oleksandrathedest
Предмет: Математика,
автор: rinka555
Предмет: История,
автор: Аноним