Предмет: Алгебра,
автор: prptptptp
Помогите доказать неравенство
Приложения:
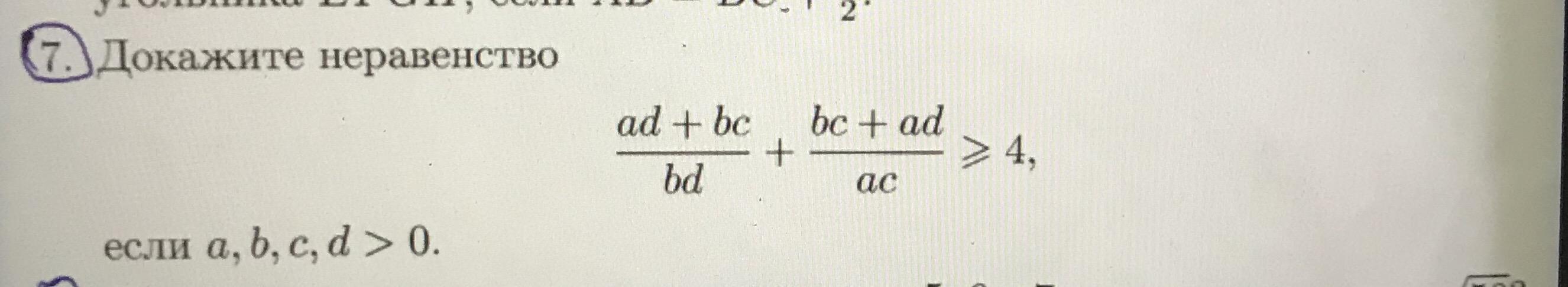
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Подготовим подстановку:
Теперь
что требовалось доказать
Похожие вопросы
Предмет: Другие предметы,
автор: bejlahanna
Предмет: Українська мова,
автор: timatimych09
Предмет: Математика,
автор: klubromanti20
Предмет: Химия,
автор: albert42