помогите найти производную
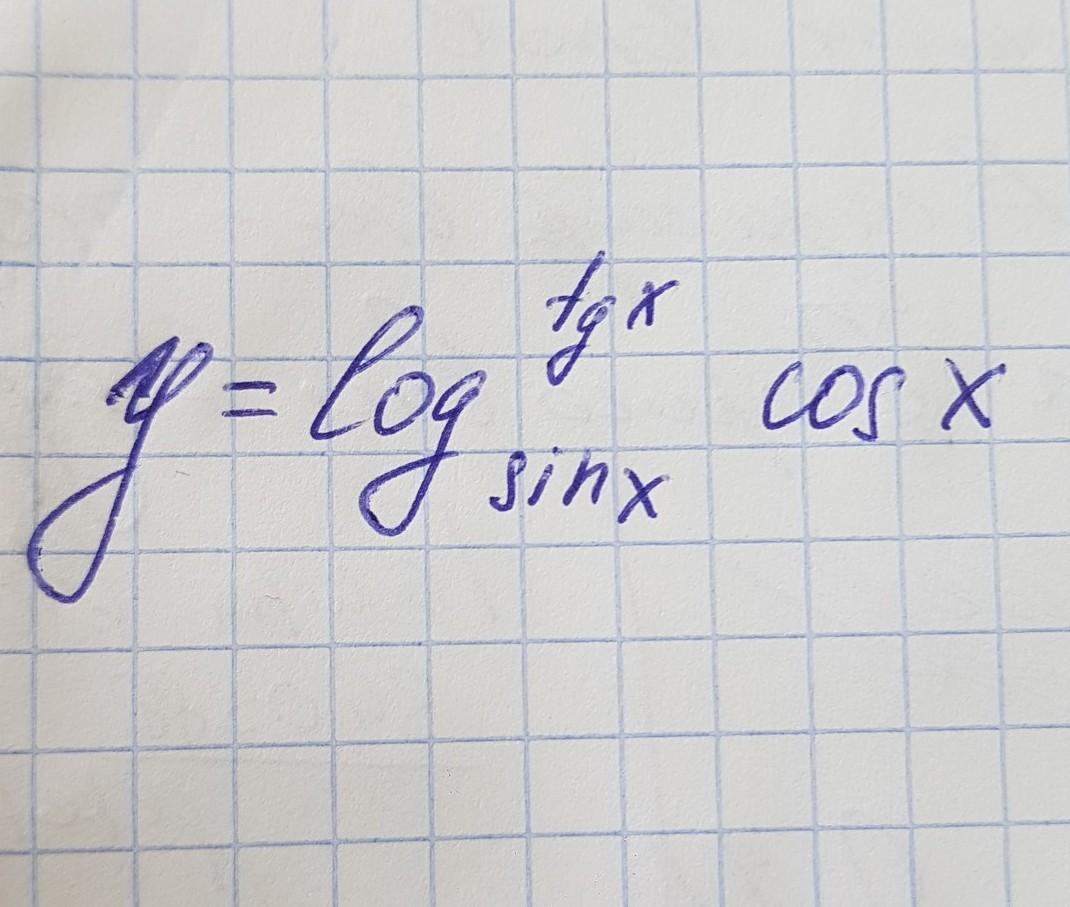
Ответы
Это сложная функция.
Производная сложной функции:
Внимательно смотрим на первую формулу. При взятии производной от сложной функции сначала производная берется по "внешней" функции, то есть той, которая вычисляется последней. И вот все то добро, которое у неё в аргументе, никуда не девается.
Формулу можно так записать, чтоб понятнее было:
Можно записать ещё дальше вложенность функций:
И так можно для любого уровня вложенности. Принцип понятен.
Вспомним пару правил нахождения производных
Запишем нашу функцию через натуральный логарифм
Имеем вообще такой вид (пока без степени):
Преобразуем чуть-чуть
где , а
.
Представим нашу функцию в несколько общем виде и найдем производную
где
Производная f(x) найдена, а для g(x):
Вычисляем производную:
Здесь разве что можно дроби на тангенс и котангенс заменить и все.