Question

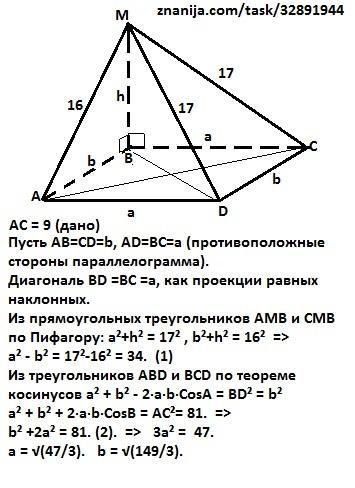
В вершине тупого угла В параллелограмма АВСД восставлен перпендикуляр ВМ к его плоскости, и точка М соединена отрезками прямых с остальными вершинами параллелограмма.
Определить стороны параллелограмма, если АМ = 16 см, МД=МС= 17 см и АС=9см​

Answer 1

Ответ:

a = √(47/3). Тогда b = √(149/3).

Объяснение:

Пусть АВ=CD=b, AD=BC=a (противоположные стороны параллелограмма).  Диагональ BD = ВС = а, как проекции равных наклонных.Из прямоугольных треугольников АМВ и СМВ по Пифагору:

а²+h² = 17² ;  b²+h² = 16²  =>

a² - b² = 17²-16² = 34.  (1)

Из треугольников АВD и BCD по теореме косинусов имеем:

a² + b² - 2·a·b·CosA = BD² = b²

a² + b² + 2·a·b·CosB = AC²= 81.  (CosB = Cos(180-A) = -CosA).  Сложим оба равенства:

2a²+2b² = b² + 81. => b² +2a² = 81. (2).

Вычтем: (1) - (2) и получим 3а² = 81-34 = 47. =>

a = √(47/3). Тогда b = √(149/3).