Question

Помогите пожалуйста.
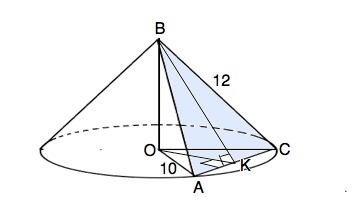
Дано:конус
треугольник ABC
равносторонний
l=12 , r=10
Найти: OK, h
решение:

Answer 1

Как правило, такое краткое условие дается с  рисунком. Понимается так: Сечение  конуса  образует равносторонний треугольник АВС  с основанием АС. Радиус основания конуса 10, образующая 12.   ОК⊥АС. Требуется найти высоту конуса ВО и длину отрезка ОК  

По условию ∆ АВС -равносторонний, боковые стороны равны 12, а диаметр основания равен 10•2=20. Следовательно, АВС не является осевым сечением конуса. Соединим центр О основания  с А и С. 

Треугольник АОС равнобедренный, АС=L=12 (из условия);   высота ОК делит его на два равных прямоугольных треугольника с гипотенузой, равной R=10, и катетами АК=АС:2=6 и ОК  (его длину нужно найти). 

Отношение АК:ОА=6:10=3:5, следовательно, ∆ АОК "египетский, его катет ОК=8 ( можно найти по т.Пифагора)

Высота  ВО конуса  перпендикулярна основанию и проецируется в его центр. ∆ ВОС - прямоугольный. Катет ОС=R=10, гипотенуза ВС=12. 

По т.Пифагора ВО=√(ВС²-ОС²)=√(144-100)=2√11