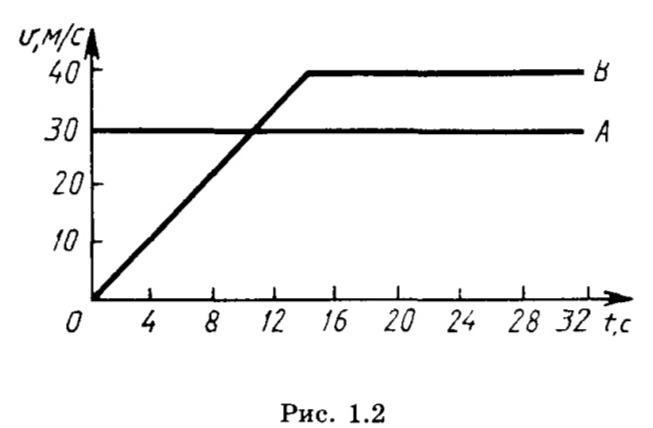
На рисунке 1.2 приведены графики скоростей двух тел A и B, движущихся прямолинейно, координаты которых в начальный момент времени t=0 совпадают. Через какое время их перемещения совпадут?
УРОВЕНЬ 10-11 КЛАСС ИЛИ УНИВЕРСИТЕТА
Ответы
Ответ:
t = 32 c
Объяснение:
по рисунку определяем
тело А
движение равномерное прямолинейное Vax = 30 м/с
тело В
движение равноускоренное прямолинейное
в момент времени to = 0 Vb(0) = 0
в момент времени t4 = 4 c Vb(4) = 10 м/с
вычисляем ускорение
a = (Vb(4) -Vb(0) ) / (t4-to) = (10 -0 ) / (4-0) = 2,5 м/с2
время t1, когда скорость тела В достигла Vb(t1) = 40 м/с
t1 = (Vb(t1) -Vb(0) ) / a = (40 - 0 ) / 2,5 = 16 c
перемещение тел за время t1 = 16 c
Sa(t1) = Vax * t1 = 30* 16 = 480 м
Sb(t1) = (Vb(t1))²/ (2 a) = 40²/ (2*2,5) = 320 м
после t1 = 16 c
движение тела В равномерное прямолинейное Vbx = 40 м/с
тело В отстает от тела А на S = Sa(t1) - Sb(t1) =480 - 320 = 160 м
скорость тела В относительно тела А
Vbax = Vbx - Vax = 40 - 30 = 10 м/с
время нагона
t2 = S / Vbax = 160 / 10 = 16 c
время, когда перемещения тел А и В совпадут
t = t1 +t2 = 16 + 16 = 32 c