Предмет: Алгебра,
автор: Wumpscut
Докажите неравенство
Приложения:
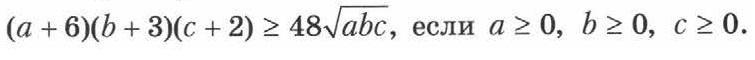
Ответы
Автор ответа:
1
Доказать неравенство: (a+6)(b+3)(c+2) ≥ 48√(abc), если a, b, c ≥ 0
Доказательство:
Для неотрицательных a,b,c применим неравенство Коши
Перемножив все эти три неравенства, мы получаем
Доказано.
Похожие вопросы
Предмет: Математика,
автор: SkReP04kaa
Предмет: Биология,
автор: kushnirmargo83
Предмет: Алгебра,
автор: Xelga1307
Предмет: Химия,
автор: tvoyamilka
Предмет: Литература,
автор: урас