Предмет: Математика,
автор: daniel397
ПОМОГИТЕ ПОЖАЛУЙСТА, СРОЧНО!!!!
1)Указать комплексное число на плоскости C, перевести в другую форму.
2)Найти модуль и аргумент комплексного числа z
3)Решить уравнение
4)Вычислить
Приложения:
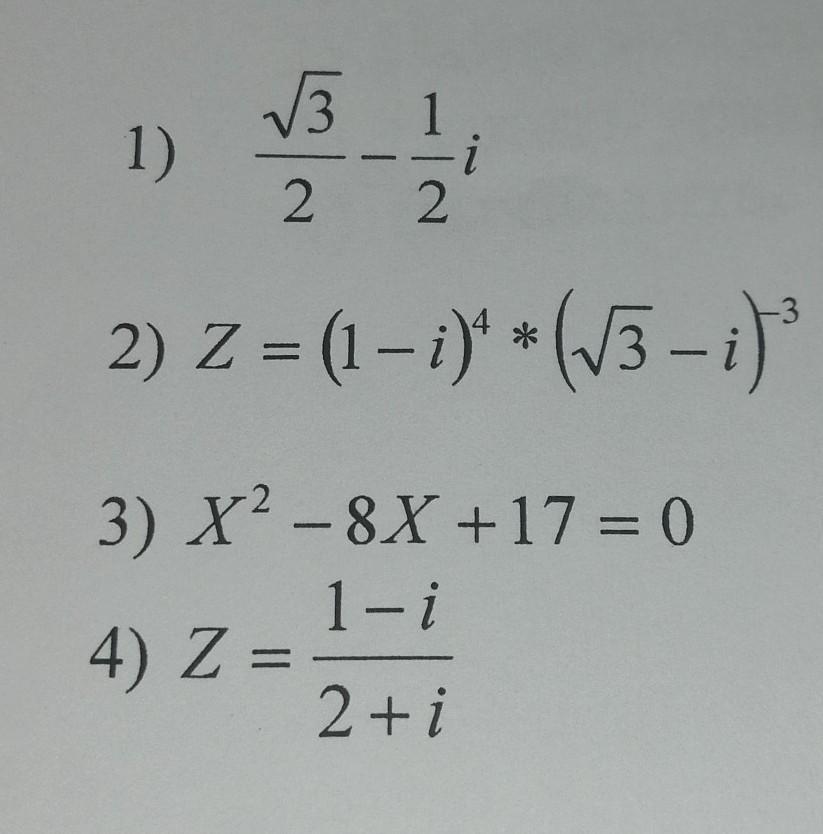
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: История,
автор: vika851352
Предмет: Математика,
автор: tasbolatovasadiar596
Предмет: Алгебра,
автор: uliana08042008
Предмет: Математика,
автор: Баса0