Предмет: Алгебра,
автор: karimkuralay
Пожалуйста помогите, нужно доказать тождество плиз срочно! Люди добрые помогите!
Приложения:
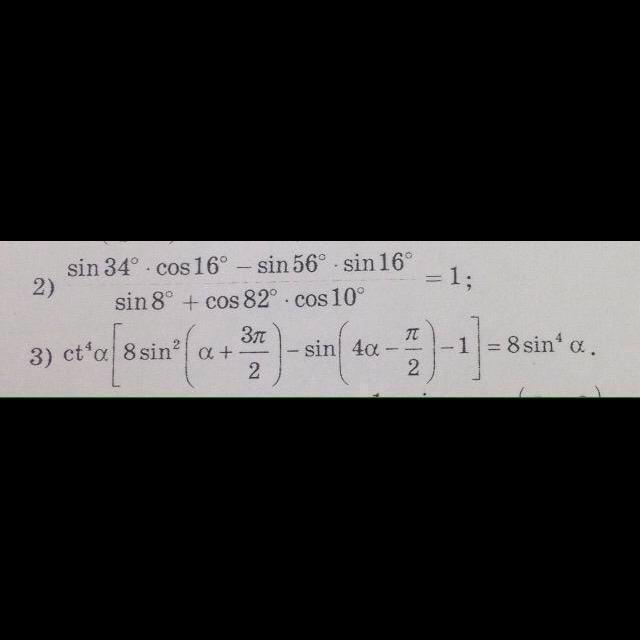
Universalka:
В заданиях опечатки
Спасибо
Пожалуйста
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Музыка,
автор: incorrp027
Предмет: Английский язык,
автор: user248
Предмет: Английский язык,
автор: gerel38
Предмет: Литература,
автор: урас
Предмет: История,
автор: 55E