Предмет: Алгебра,
автор: MarsHack2002
Докажите, что функция y=cos(5x+П/4) является периодической с периодом Т=2П/5
Ответы
Автор ответа:
2
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!!
Приложения:
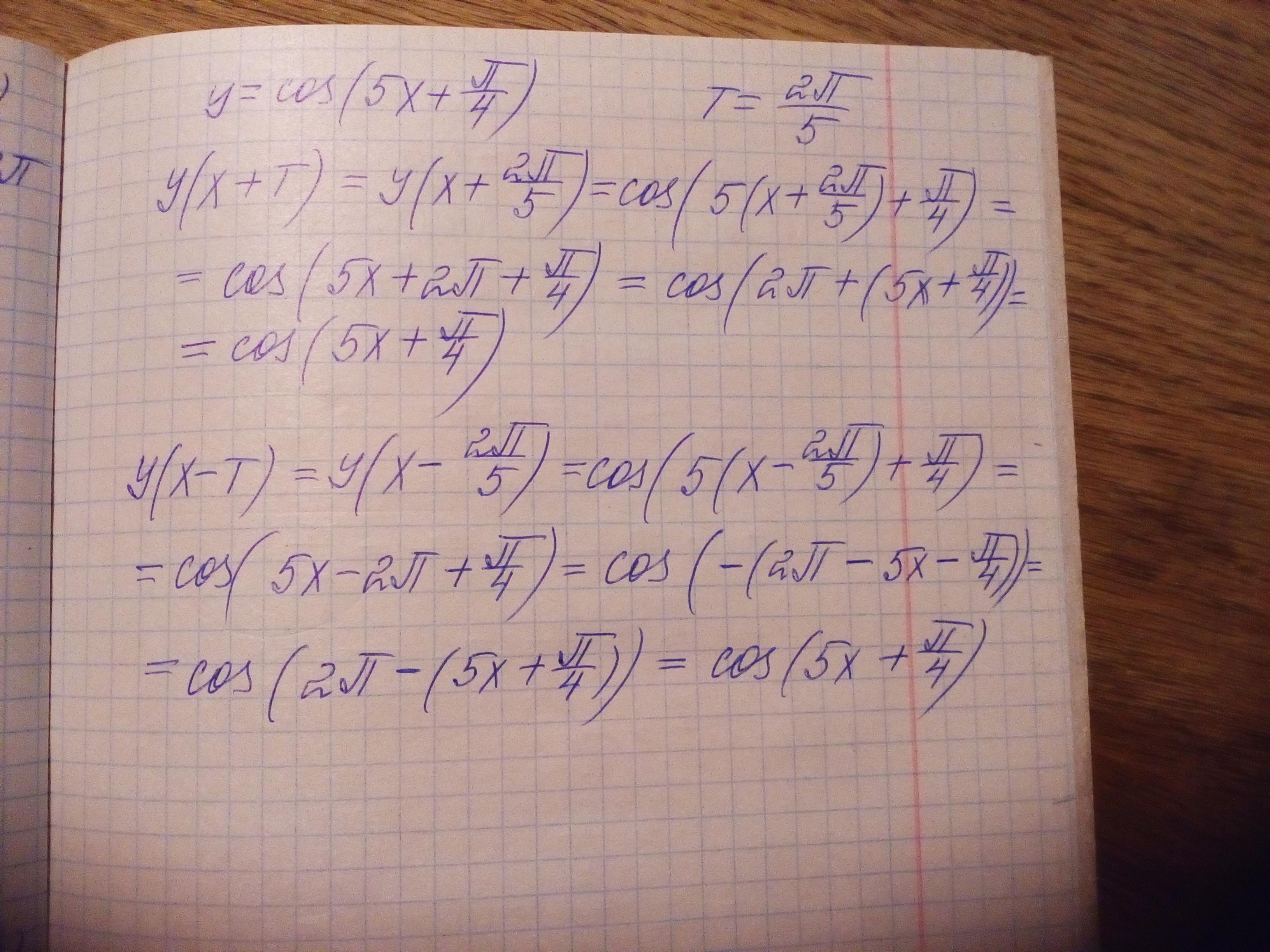
Автор ответа:
1
Ответ:
1 способ:
y = cos (5x + π/4)
Если Т = 2π/5 - период этой функции, то у(х) = у(х + Т). Проверим:
y(x + T) = cos (5(x + T) + π/4) = cos (5(x + 2π/5) + π/4) =
= cos (5x + 2π + π/4) = cos (5x + π/4) = y(x)
Верно. Значит Т = 2π/5 - период этой функции.
2 способ:
Найдем период функции y = cos (5x + π/4).
Для этого в формулу, задающую функцию, вместо х подставим (х + Т):
y(x + T) = cos (5(x + T) + π/4) = cos (5x + 5T + π/4) = cos (x + π/4 + 5T)
Наименьший положительный период функции у = cosx равен 2π, значит
5T = 2π
T = 2π/5
Похожие вопросы
Предмет: Биология,
автор: oksanaion1985
Предмет: Химия,
автор: 12yuyu
Предмет: Математика,
автор: dilnazkuanyshbai
Предмет: Математика,
автор: buerova1997