Предмет: Математика,
автор: kaneki13449047
Помогите пожалуйста решить с помощью формулы:
Приложения:
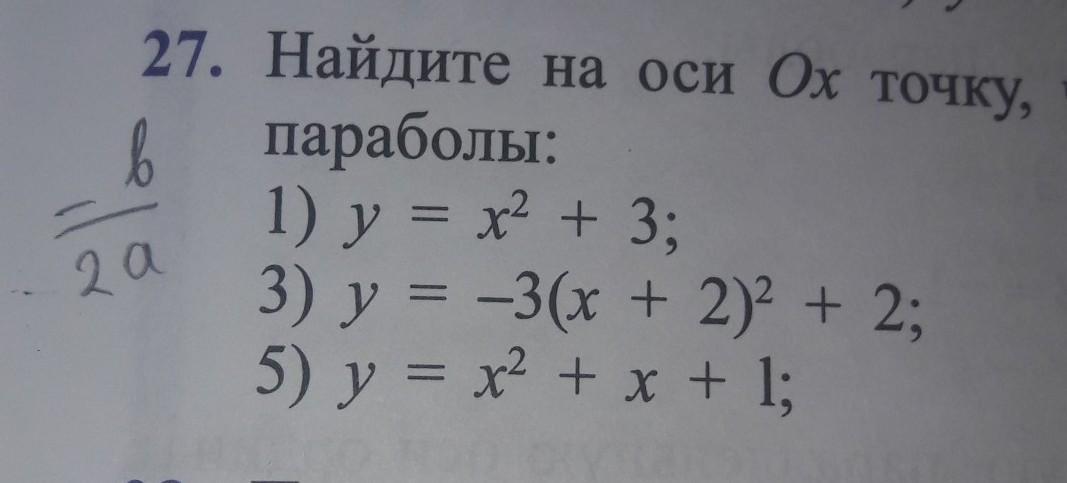
Ответы
Автор ответа:
1
Ответ:
Ось симметрии параболы, заданной уравнением y=ax^2+bx+c проходит через её вершину, параллельно оси OY. Т. е. для того, чтобы найти точку, через которую она проходит, нужно найти абсциссу вершины параболы. Её можно найти по формуле \frac{-b}{2a}.
1. x = 0;
2. x = -2;
3. x = -0,5
Y=x²+2x-6
Ось симметрии параболы проходит через абсциссу вершины параболы параллельно оси Оу.
х (в) =-2/2=-1
Следовательно, уравнение х=-1 и есть ось симметрии параболы.
Точка (-1;0) - точка пересечения параболы с осью Ох
Пошаговое объяснение:
kaneki13449047:
а решение какое?
скажите пожалуйста
по маленькой формуле
-b дробь 2а
Похожие вопросы
Предмет: Английский язык,
автор: girl1528
Предмет: Математика,
автор: qazqazvetalplmplm
Предмет: Математика,
автор: viktorianikto23
Предмет: Биология,
автор: Mariyazh
Предмет: Математика,
автор: orlovchanka2309