Предмет: Алгебра,
автор: mike45388
Доказать методом математической индукции, что:
см. 23 номер
Приложения:
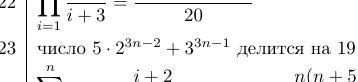
Ответы
Автор ответа:
1
Доказать что число 5 * 2^(3n-2) + 3^(3n-1) делится на 19
Доказательство:
1) База индукции: n = 1
2) Предположим что и при выражение
3) Индукционный переход: n = k+1
Первое слагаемое делится на 19 по предположению (второй пункт), а второе слагаемое очевидно что делится на 19, так как имеет сомножитель 19.
Похожие вопросы
Предмет: Русский язык,
автор: vvww5610
Предмет: Математика,
автор: leonovec24
Предмет: Физика,
автор: keykey2
Предмет: Математика,
автор: макс2065
Предмет: Литература,
автор: tumasyansir