Предмет: Геометрия,
автор: polovodin2019
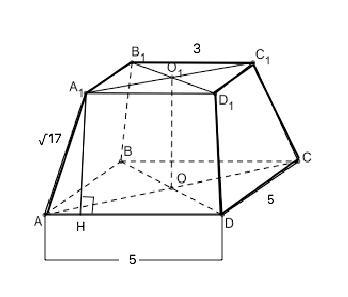
Стороны оснований правильной четырехугольной усеченной пирамиды равны 5 и 3.
Ребро усеченной пирамиды равно  .
.
Найти площадь её полной поверхность.
Ответы
Автор ответа:
7
Ответ: 98
Объяснение:
Поверхность правильной четырехугольной усеченной пирамиды состоит из двух оснований-квадратов и четырех равных боковых граней- равнобедренных трапеций.
Площадь трапеции равна произведению полусуммы оснований на высоту.
Опустим из вершины А1 боковой грани АА1D1D высоту А1Н на АD. Высота равнобедренной трапеции из тупого угла делит основание на отрезки, меньший из которых равен полуразности оснований, больший - их полусумме.
АН=(АD-А1D1):2=(5-3):2=1
Треугольник АА1Н - прямоугольный. По т.Пифагора А1Н=√(AA1²-AH²)=√(17-1)=4
S(осн)=S(ABCD)+S(A1B1C1D1)=5²+3²=34 (ед. площади)
S(бок)=4•S(AA1D1D)=4•0,5•(3+5)•4=64(ед. площади)
Ѕ(полн)=34+64=98 (ед. площади)
Приложения:
Похожие вопросы
Предмет: Математика,
автор: pq24xymxwx
Предмет: Математика,
автор: RauAn1267
Предмет: Математика,
автор: aspect57161
Предмет: Литература,
автор: Eldar2012