Здравствуйте, помогите пожалуйста, что только не пробовал, не получается сделать. Нужно решить это уравнение через формулы в Excel. И должны получиться значения. У меня получилось вот такая формула, но чего-то не хватает, не пойму чего.
=ЕСЛИ(ИЛИ(A2<-8;A2>=1;A2<>3;A2<>2;A2<=4);A2*EXP(1)^1/A2^2);ЕСЛИ(ИЛИ(A2<1;A2>=-4;A2=3);СУММ(1/TAN(СУММ(A2^2;5));TAN(СУММ(A2;4,5))^2));ЕСЛИ(ИЛИ(A2>4;A2<>7;A2=-5);КОРЕНЬ(СУММ(ABS(A2)/3;A2*A2)));ЕСЛИ(ИЛИ(A2<-4;A2=7;A2<>-5;A2>=-8);LOG(A2*A2*A2*A2;4))
Вот условие, а на скриншоте ниже, само уравнение.
Задание1. Расставить согласующиеся логические элементы в условиях и выполнить расчет у для целых значений x от -15 до 15. Условия не должны противоречить друг другу. Задания по вариантам указаны в табл. 1.
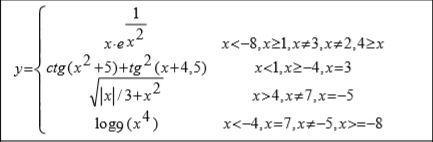
Ответы
Первый столбец - начиная с A14 по A44
Второй столбец - начиная с B14 по B44
В первом размещаем числа от 15 до 15 (значения аргумента)
В B14 пишем формулу =A14*EXP(1/A14^2)*(ЦЕЛОЕ((2-ЗНАК(A14-4))/2)*ЦЕЛОЕ((2+ЗНАК(A14-1))/2)*ABS(ЗНАК(A14-3))*ABS(ЗНАК(A14-2))+ЦЕЛОЕ((1-ЗНАК(A14+8))/2))+(1/TAN(A14^2+5)+(TAN(A14+4,5))^2)*(ЦЕЛОЕ((1-ЗНАК(A14-1))/2)*ЦЕЛОЕ((2+ЗНАК(A14+4))/2)+1-ABS(ЗНАК(A14-3)))+(ABS(A14)/3+A14^2)^0,5*(ЦЕЛОЕ((1+ЗНАК(A14-4))/2)*ABS(ЗНАК(A14-7))+1-ABS(ЗНАК(A14+5)))+LOG(A14^4;9)*(ЦЕЛОЕ((1-ЗНАК(A14+4))/2)*ЦЕЛОЕ((2+ЗНАК(A14+8))/2)*ABS(ЗНАК(A14+5))+1-ABS(ЗНАК(A14-7)))
И растягиваем ее вниз до B44
Получаем два вот таких столбца (обратите внимание, при аргументе равном нулю возникает ошибка деления на ноль):
-15 -15,06681503
-14 -14,0716111
-13 -13,07715111
-12 -12,08362336
-11 -11,09128579
-10 -10,10050167
-9 -9,111799813
-8 3,785578521
-7 3,542487498
-6 3,261859507
-5 5,163977795
-4 -0,356218705
-3 198,9880782
-2 -1,652803098
-1 -3,296038602
0 #ДЕЛ/0!
1 2,718281828
2 0
3 7,460544767
4 4,257977836
5 5,163977795
6 6,164414003
7 3,542487498
8 8,164965809
9 9,16515139
10 10,16530045
11 11,16542282
12 12,16552506
13 13,16561177
14 14,16568624
15 15,16575089
Формула незамысловатая, но занудная от однообразия.
Выводится следующим образом.
1) Выписываем четыре формулы и выясняем область определения для каждой из функций.
2) Для границ и отдельных значений из области определения описываем отдельную функцию Хевисайда, которая принимает значение 1 при соблюдении условия и 0 при несоблюдении условия.
3) Компонуем полученные функции по "И" и "ИЛИ" (умножить или сложить), получаем бинарную функцию.
4) Умножаем каждую из четырех формул на соответствующую бинарную функцию.
5) Складываем полученные произведения.