Предмет: Алгебра,
автор: svetagerb78
Помогите решить дифференциальные уравнения, пожалуйста
Приложения:
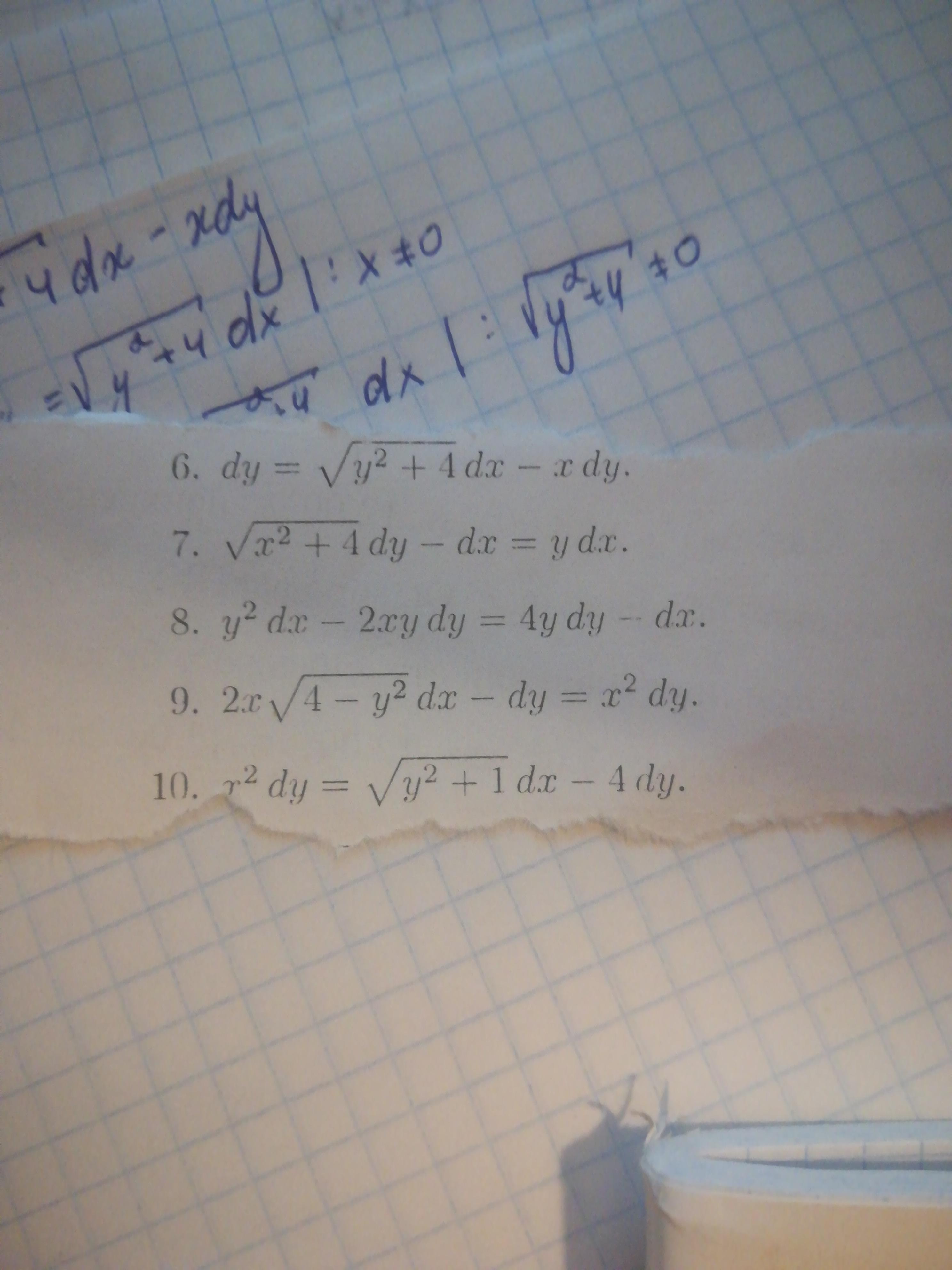
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: История,
автор: crip4175
Предмет: Литература,
автор: klimenkonazar632
Предмет: Русский язык,
автор: Safaa771
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: Dianachka555