Предмет: Геометрия,
автор: daniilmakriz
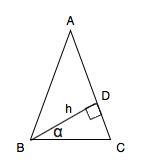
В равнобедренном треугольнике высота, проведённая к боковой стороне, равна
h и образует с основанием угол α. Найти площадь треугольника.
Ответы
Автор ответа:
0
Ответ:
Объяснение:
BD = h, ∠DBC=α , AB = AC = x, BD - высота, S=?
1) BD - высота => BD⊥AC => ∠BDC = ∠BDA = 90°
2) В ΔBDC ∠BDC=90° => ∠BCD = 90° - α
3) В ΔBAC ∠BAC = 180° - ∠ABC - ∠BCA = 180° - 2∠BCA = 180° - 2(90° - α) = 180° - 180° + 2α = 2α
4) В ΔBDA ∠BDA=90° =>
5)
Приложения:
Похожие вопросы
Предмет: Химия,
автор: Аноним
Предмет: Математика,
автор: bisesra654
Предмет: Биология,
автор: palinka98084
Предмет: Литература,
автор: Sleepground