Предмет: Алгебра,
автор: TochkaDostupa1
Найти полный дифференциал
Приложения:
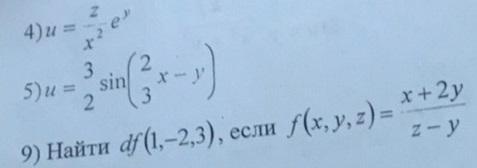
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: История,
автор: vlulall80
Предмет: Русский язык,
автор: temirbaevaanastasia
Предмет: Математика,
автор: zholodenkodiana
Предмет: Биология,
автор: дарина1471
Предмет: Химия,
автор: sokolova2012mar