Question

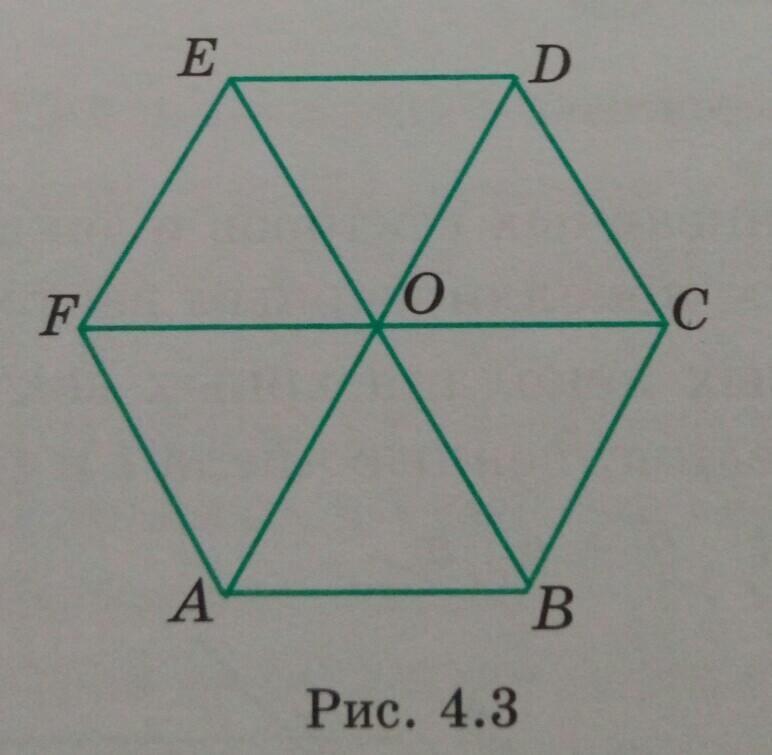
Диагонали правильного шестиугольника ABCDEF пересекаются в точке О(рис. 4.3). Найдите такие числа t, s, для которых:
а) AC = t . AB + ѕ. AD;
б) AD = t. AB + ѕ. AF;
в) AE = t - AD + s. BЕ​

Answer 1

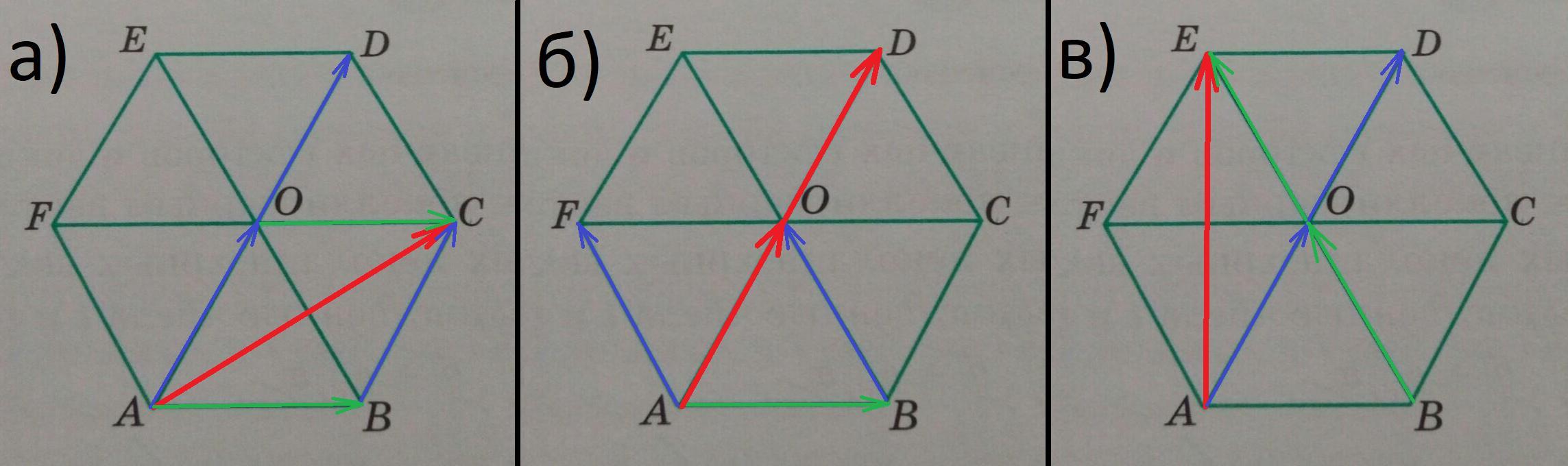
Большие диагонали правильного шестиугольника, делят его на 6 правильных треугольников, поэтому AOCB и AFOB параллелограммы (по попарно равным сторонам).

а)

$\vec{AC} =\vec{AB} +\vec{AO} =1\cdot \vec{AB} +\dfrac12 \cdot \vec{AD}$

Первый переход верен по правилу параллелограмма.

t = 1;  s = 0,5.

б)

$\vec{AD} =2\cdot \vec{AO} =2\cdot (\vec{AB}+\vec{BO}) =2\cdot \vec{AB} +2\cdot \vec{AF}$

Второй переход верен по правилу треугольника, а третий по правилу параллелограмма.

t = 2;  s = 2.

в)

$\vec{AE} =\vec{AO} +\vec{OE} =\dfrac12 \cdot \vec{AD} +\dfrac12 \cdot \vec{BE}$

Первый переход верен по правилу треугольника.

t = 0,5;  s = 0,5.