Предмет: Геометрия,
автор: gataulin83
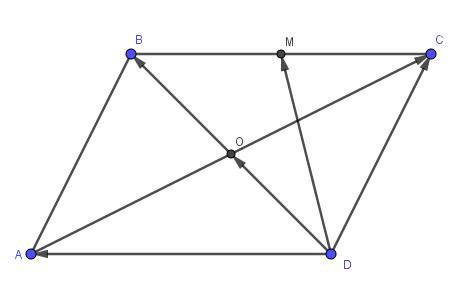
ABCD - параллелограмм, M - середина BC. Выразить (над всем дальше вектора) DO, DM, AC через a = DC;b=DA
Аноним:
Что такое О?
Ответы
Автор ответа:
32
Рассмотрим треугольник ABD: по правилу треугольника
O - точка пересечения диагоналей параллелограмма и делит она диагонали пополам, значит
Поскольку М - середина, то она делит BC пополам.
По правилу треугольника из треугольника DMC
Из треугольника ACD по правилу треугольника
Приложения:
извините, не могли бы вы добавить решение к моей задаче
Похожие вопросы
Предмет: Русский язык,
автор: denislutsyshyn1
Предмет: Химия,
автор: karapyziik
Предмет: История,
автор: ylianarawrenchuk
Предмет: Математика,
автор: Rodion2017
Предмет: Физика,
автор: cAreOnAir