Предмет: Алгебра,
автор: alenavolkova9
Помогите с lim(3-5)^4 - (2-n)^4)/(1-n)^3 - (1+n)^3
Приложения:
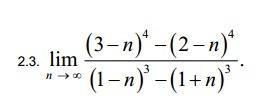
Ответы
Автор ответа:
1
Аноним:
во второй строчке в знаменателе не закрыта скобка.
Похожие вопросы
Предмет: Алгебра,
автор: darysha005
Предмет: Математика,
автор: glebkonoplev822
Предмет: Математика,
автор: alenkaakovec12
Предмет: Математика,
автор: Dasha151315
Предмет: Биология,
автор: помогуна51