Предмет: Геометрия,
автор: УДаФ
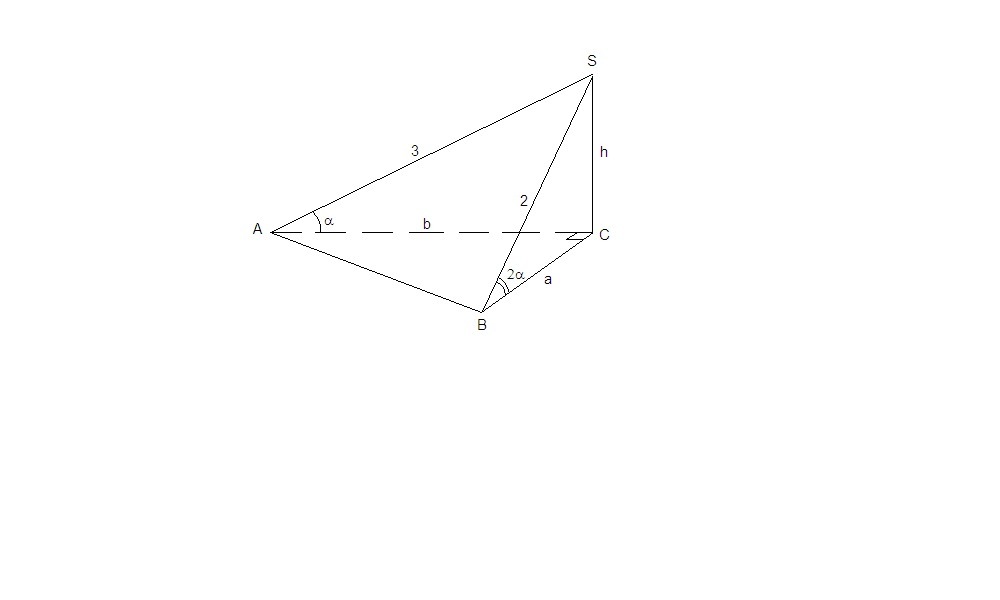
Основанием пирамиды служит прямоугольный треугольник; боковые грани, проходящие через его катеты, перпендикулярны к плоскости основания. Наклонные боковые ребра равны 2дм и 3дм, они образуют с плоскостью основания углы, которые относятся как 2:1. Найдите объем пирамиды
Ответы
Автор ответа:
0
Так как две боковые грани перпендикулярны основанию, то боковое ребро, проходящее через вершину прямого угла, перпендикулярно основанию, т.е. является высотой пирамиды.
sin∠SAC = h/3
sin∠SBC = h/2, значит ∠SAC < ∠SBC.
Обозначим ∠SAC = α, тогда ∠SBC = 2α.
h = 3sinα
h = 2sin2α, получаем уравнение:
3sinα = 2sin2α
3sinα - 2sin2α = 0
3sinα - 4sinα·cosα = 0 (так как sin2α = 2sinα·cosα)
sinα·(3 - 4cosα) = 0
sinα = 0 или 3 - 4cosα = 0
α = 0 - не подходит, cosα = 3/4
sinα = √(1 - cos²α) = √(1 - 9/16) = √7 / 4
h = 3√7/4 дм
Найдем катеты основания:
b = 3cosα = 9/4 дм
a = 2cos2α = 2(2cos²α - 1) = 2(2·9/16 - 1) = 1/4 дм
Sосн = 1/2 ab = 1/2 · 1/4 · 9/4 = 9/32 дм²
V = 1/3 Sосн·h = 1/3 · 9/32 · 3√7/4 = 9√7/128 дм³
sin∠SAC = h/3
sin∠SBC = h/2, значит ∠SAC < ∠SBC.
Обозначим ∠SAC = α, тогда ∠SBC = 2α.
h = 3sinα
h = 2sin2α, получаем уравнение:
3sinα = 2sin2α
3sinα - 2sin2α = 0
3sinα - 4sinα·cosα = 0 (так как sin2α = 2sinα·cosα)
sinα·(3 - 4cosα) = 0
sinα = 0 или 3 - 4cosα = 0
α = 0 - не подходит, cosα = 3/4
sinα = √(1 - cos²α) = √(1 - 9/16) = √7 / 4
h = 3√7/4 дм
Найдем катеты основания:
b = 3cosα = 9/4 дм
a = 2cos2α = 2(2cos²α - 1) = 2(2·9/16 - 1) = 1/4 дм
Sосн = 1/2 ab = 1/2 · 1/4 · 9/4 = 9/32 дм²
V = 1/3 Sосн·h = 1/3 · 9/32 · 3√7/4 = 9√7/128 дм³
Приложения:
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Химия,
автор: Аноним
Предмет: Английский язык,
автор: stoyanovakate1
Предмет: Математика,
автор: Путилова
Предмет: Математика,
автор: ХУЛИгонка