Предмет: Алгебра,
автор: submarsist
Помогите решить выражение с кубическим корнем, пожалуйста :)
Приложения:
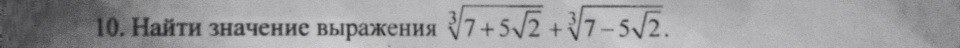
Ответы
Автор ответа:
0
Возведём в куб заданное выражение по формуле 
![(sqrt[3]{7+5sqrt2}+sqrt[3]{7-5sqrt2})^3=\\=7+5sqrt2+7-5sqrt2+3sqrt[3]{(7+5sqrt2)(7-5sqrt2)}cdot (sqrt[3]{7+5sqrt2}+sqrt[3]{7-5sqrt2})=\\=14+3sqrt[3]{49-50}(sqrt[3]{7+5sqrt2}+sqrt[3]{7-5sqrt2})=\\=14-3(sqrt[3]{7+5sqrt2}+sqrt[3]{7-5sqrt2}) (sqrt[3]{7+5sqrt2}+sqrt[3]{7-5sqrt2})^3=\\=7+5sqrt2+7-5sqrt2+3sqrt[3]{(7+5sqrt2)(7-5sqrt2)}cdot (sqrt[3]{7+5sqrt2}+sqrt[3]{7-5sqrt2})=\\=14+3sqrt[3]{49-50}(sqrt[3]{7+5sqrt2}+sqrt[3]{7-5sqrt2})=\\=14-3(sqrt[3]{7+5sqrt2}+sqrt[3]{7-5sqrt2})](https://tex.z-dn.net/?f=%28sqrt%5B3%5D%7B7%2B5sqrt2%7D%2Bsqrt%5B3%5D%7B7-5sqrt2%7D%29%5E3%3D%5C%5C%3D7%2B5sqrt2%2B7-5sqrt2%2B3sqrt%5B3%5D%7B%287%2B5sqrt2%29%287-5sqrt2%29%7Dcdot+%28sqrt%5B3%5D%7B7%2B5sqrt2%7D%2Bsqrt%5B3%5D%7B7-5sqrt2%7D%29%3D%5C%5C%3D14%2B3sqrt%5B3%5D%7B49-50%7D%28sqrt%5B3%5D%7B7%2B5sqrt2%7D%2Bsqrt%5B3%5D%7B7-5sqrt2%7D%29%3D%5C%5C%3D14-3%28sqrt%5B3%5D%7B7%2B5sqrt2%7D%2Bsqrt%5B3%5D%7B7-5sqrt2%7D%29)
Переобозначим исходное выражение за t. Это же выражение записано в скобке,
получим

Раз 2 - корень кубического многочлена, то многочлен должен делиться нацело на разность t-2.Получим
![t^3+3t-14=(t-2)(t^2+2t+7)\t^2+2t+7=0\D=4-4cdot 7=-24<0; to ; net ; resenij; to \t-2=0,; t=2; to \sqrt[3]{7+5sqrt2}+sqrt[3]{7-5sqrt2}=2 t^3+3t-14=(t-2)(t^2+2t+7)\t^2+2t+7=0\D=4-4cdot 7=-24<0; to ; net ; resenij; to \t-2=0,; t=2; to \sqrt[3]{7+5sqrt2}+sqrt[3]{7-5sqrt2}=2](https://tex.z-dn.net/?f=t%5E3%2B3t-14%3D%28t-2%29%28t%5E2%2B2t%2B7%29%5Ct%5E2%2B2t%2B7%3D0%5CD%3D4-4cdot+7%3D-24%26lt%3B0%3B+to+%3B+net+%3B+resenij%3B+to+%5Ct-2%3D0%2C%3B+t%3D2%3B+to+%5Csqrt%5B3%5D%7B7%2B5sqrt2%7D%2Bsqrt%5B3%5D%7B7-5sqrt2%7D%3D2)
Переобозначим исходное выражение за t. Это же выражение записано в скобке,
получим
Раз 2 - корень кубического многочлена, то многочлен должен делиться нацело на разность t-2.Получим
Похожие вопросы
Предмет: Алгебра,
автор: baukareal
Предмет: Математика,
автор: rataiarvoaoata
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: 121280