Question

Докажите, что если в трапеции диагонали равны, то трапеция равнобедренная. Выполните необходимые построения. 

Answer 1

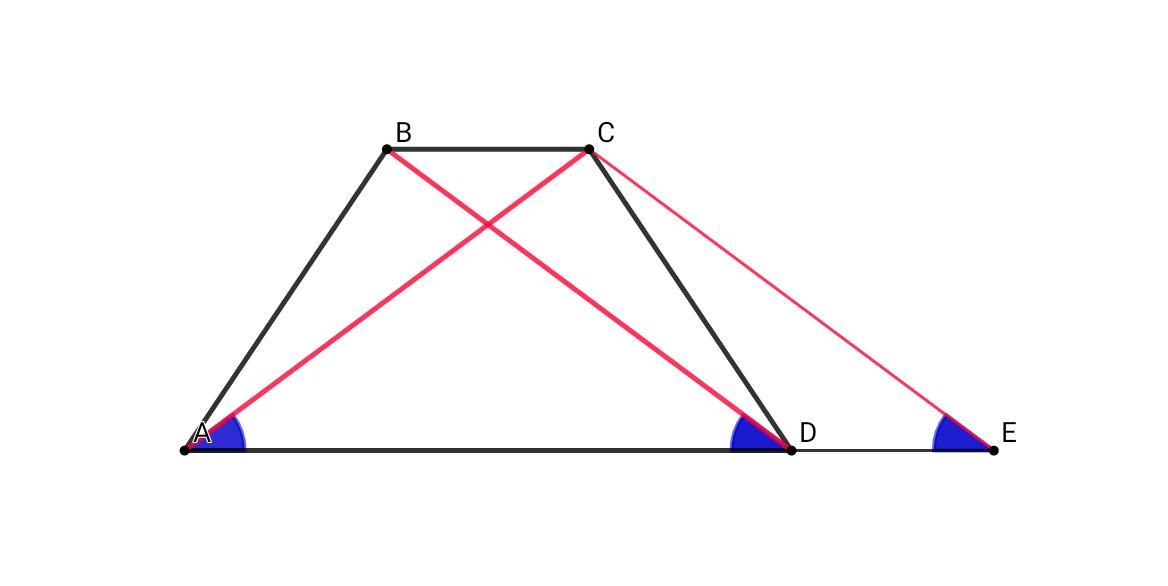
Проведём из точки С прямую СЕ, параллельную диагонали BD ⇒ BCED - параллелограмм (BD || CE , BC || DE)

AC = BD = CE ⇒ ΔACE - равнобедренный, ∠САЕ = ∠СЕА

∠BDA = ∠CEA - как соответственные углы при BD || CE и секущей AE ⇒ ∠BDA = ∠CEA = ∠CAE ⇒ ∠CAD = ∠BDA

ΔABD = ΔDCA по двум сторонам и углу между ними (AC = BD - по условию, AD - общая сторона, ∠CAD = ∠BDA)

Значит, АВ = CD ⇒ ABCD - равнобедренная трапеция, ч.т.д.

Answer 2

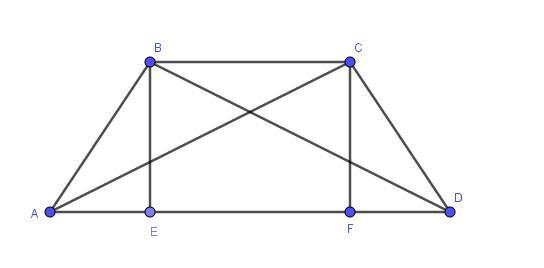
Проведем к стороне большего основания высоты BE и CF. Рассмотрим прямоугольные треугольники BED и AFC у них AC = BD (по условию), BE = CF (так как EBCF прямоугольник) ⇒ ΔBED = ΔAFC по катету и гипотенузе, следовательно AF = DE.

Заметим, что AE = AF - EF и FD = DE - EF, отсюда AE = FD.

Рассмотрим теперь прямоугольные треугольники ABE и CFD

у них BE = EF и AE = FD  ⇒  ΔABE = ΔCFD  ⇒  AB = CD следовательно, трапеция ABCD - равнобедренная