Предмет: Алгебра,
автор: МaximД
Вычислите значение выражения: 
Желательно на бумаге решить со всеми действиями.
Результат один и тот же♀️
Способы решения разные..))
В первом способе я так же сделала)
Я не спорю..))
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Автор ответа:
2
Или так:
Приложения:
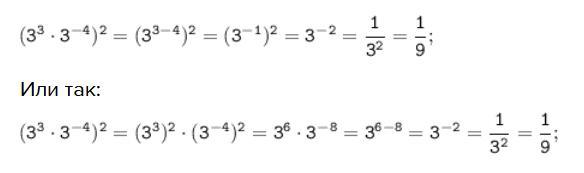
Похожие вопросы
Предмет: Математика,
автор: zblack4264
Предмет: Другие предметы,
автор: tumunov2269
Предмет: Українська література,
автор: bladkatz6102
Предмет: Алгебра,
автор: bogdansmirnov
Или так:
(3³ · 3⁻⁴)² = (3³)² · (3⁻⁴)² = 3⁶ · 3⁻⁸ = 3⁶⁻⁸ = 3⁻² = 1/9