Question

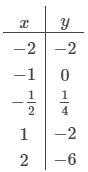
Исследуйте функцию y=-x-x^2 на чётность , непрерывность и постройте её график​

Answer 1

Ответ: Функция не является четной или нечетной. Она непрерывна.

Пошаговое объяснение:

Исследуем на чётность.

1. Запишем уравнение в виде функции от x.

$f(x)=-x-x^2$

2. Найдем $f(-x)$:

    а) Найдем $f(-x)$, подставив -x везде вместо x в $f(x)$.

$f(-x)=-(-x)-(-x)^2$

    б) Упростим каждый член:

         1) Умножаем $-(-x)$:

              1а) Умножим -1 на 1.

$f(-x)=1x-(-x)^2$

              1б) Умножим x на 1.

$f(-x)=x-(-x)^2$

         2) Применим правило произведения к -x.

$f(-x)=x-((-1)^2x^2)$

         3) Умножим -1 на $(-1)^2$, складывая показатели степеней:

               3а) Переносим $(-1)^2$

$f(-x)=x+(-1)^2\times(-1x)^2$

               3б) Умножим $(-1)^2$ на -1.

                   3б.1) Возведем -1 в степень 1.

$f(-x)=x+(-1)^2\times((-1)x^2)$

                   3б.2) Воспользуемся правилом степеней $a^ma^n=a^{m+n}$ для объединения показателей.

$f(-x)=x+(-1)^{2+1}x^2$

               3в) Складываем 2 и 1.

$f(-x)=x+(-1)^3x^2$

         4) Возведем -1 в степень 3.

$f(-x)=x-x^2$

3. Функция является четной, если $f(-x)=f(x)$.

    а) Проверим, справедливо ли $f(-x)=f(x)$

$x-x^2\neq -x-x^2$

    Поскольку $x-x^2\neq -x-x^2$, функция не является четной. Функция не является четной.

4. Функция является нечетной, если $f(-x)=-f(x)$:

    а) Найдем $-f(x)$.

         1) Умножим $-x-x^2$ на -1.

$-f(x)=-(-x-x^2)$

         2) Применяем распределительный (дистрибутивный закон).

$-f(x)=x+x^2$

    Поскольку $x-x^2 \neq x+x^2$, функция не является нечетной.

Функция не является нечетной.

Функция не является четной или нечетной.

Исследуем непрерывность.

Областью определения выражения являются все вещественные числа, кроме тех, при которых выражение не определено. В данном случае нет вещественных чисел, при которых выражение было бы неопределенным.

Запись в виде интервала:

$(-\infty; \infty)$

Нотация построения множества:

$\{x|x \in \mathbb R \}$

Поскольку областью определения является вся вещественная прямая, $y=-x-x^2$ непрерывно на множестве вещественных чисел.

Непрерывно.

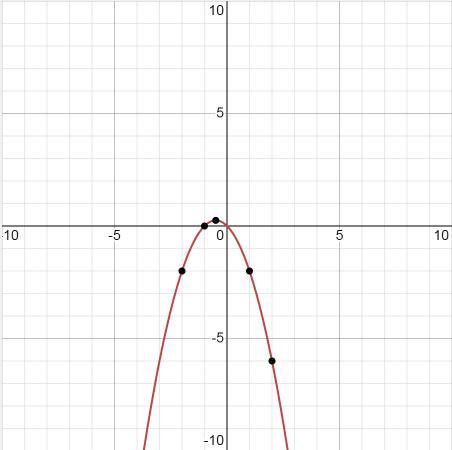
График:

Построим график параболы, используя направление ветвей, вершину, фокус и ось симметрии.

Направление: направлено вниз

Вершина: $(-\frac{1}{2} ; \frac{1}{4} )$

Фокус: $(-\frac{1}{2}; 0)$.

Ось симметрии: $x=-\frac{1}{2}$

Направляющая: $y=\frac{1}{2}$