Предмет: Геометрия,
автор: Sana0005
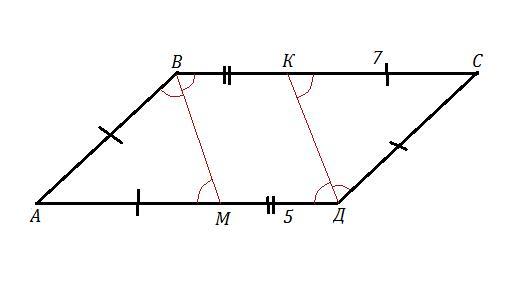
В параллелограмме ABCD биссектрисы углов ВиD пересекают стороны AD и BC в точках МиК соответственно так, что MD=5 см,
КС-7 см. Найдите периметр ABCD.
Ответы
Автор ответа:
3
АВСД - параллелограмм , ВМ и ДК - биссектрисы , то есть ∠АВМ=∠МВС , ∠АДК=∠СДК , МД=5 см , КС=7 см .
Так как в параллелограмме противоположные углы равны, то ∠В=∠Д ⇒ ∠АВМ=∠СВМ=∠АДК=∠СДК .
Но ∠АМВ и ∠АДК - соответственные равные углы ⇒ ВМ ║ДК.
Так как АВСД - параллелограмм, то ВК ║ ДМ ⇒ МВКД - тоже параллелограмм, а значит ВК=ДМ=5 см.
∠АДМ=∠ДКС как внутренние накрест лежащие при параллельных АД и ВС и секущей КД . Но ∠АДМ=∠СДК (КД - биссектриса) ⇒ ∠СДК=∠КДС , а это углы при основании ΔДСК ⇒ ΔДСК - равнобедренный ⇒ КС=СД=7 см .
Периметр параллелограмма:
Р=2*СД+2*ВС=2*7+2*(ВК+КС)=14+2*(5+7)=14+2*12=14+24=38 см .
Приложения:
Sana0005:
спасибо вам
Похожие вопросы
Предмет: Алгебра,
автор: merzlyakovavictoria2
Предмет: Английский язык,
автор: nanikovo95
Предмет: География,
автор: rparamonov2008
Предмет: Математика,
автор: бумбот
Предмет: Математика,
автор: KatyMironova