Предмет: Математика,
автор: vladonischuk
Решить уравнение : очень надо
Приложения:
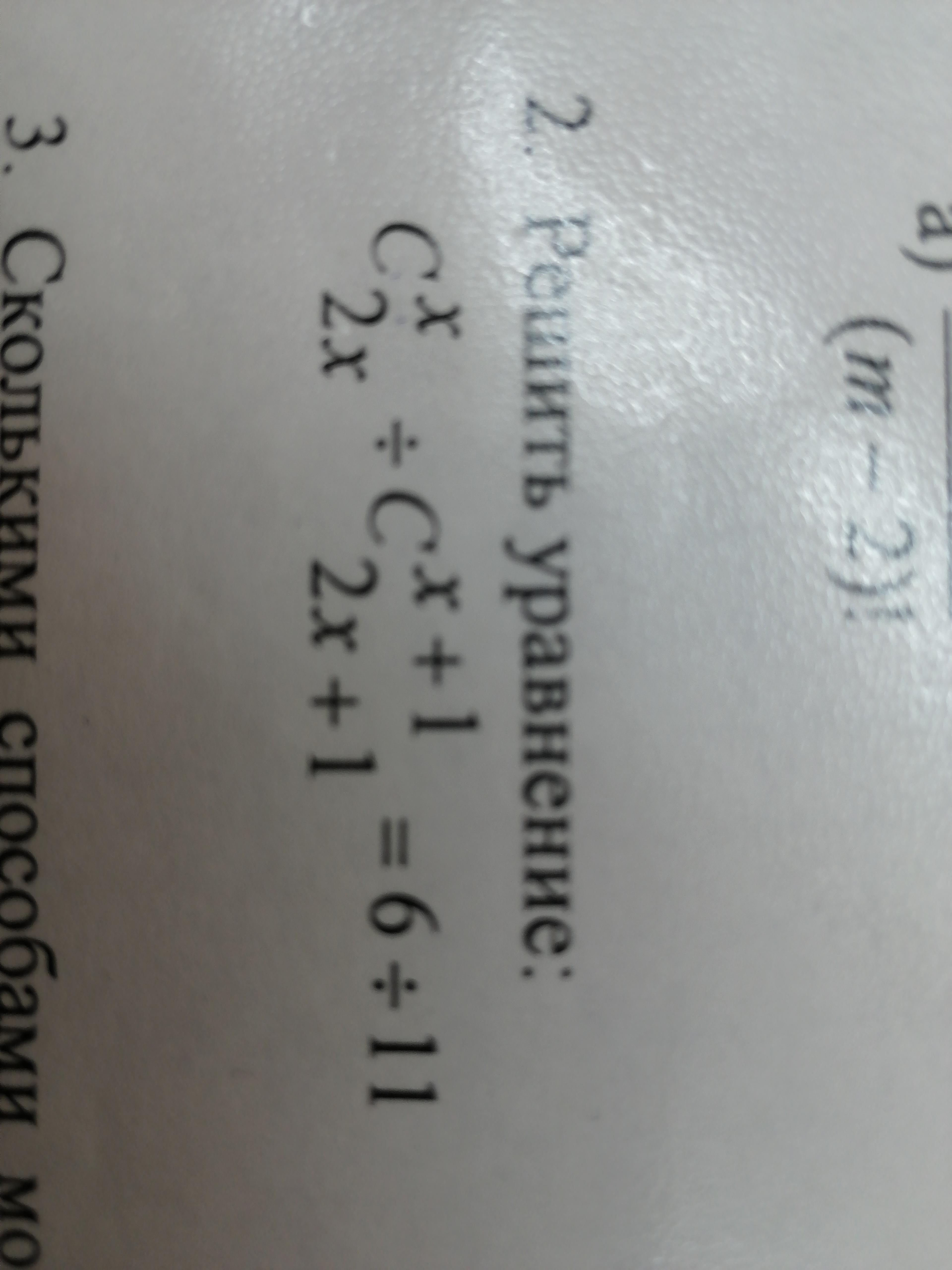
Ответы
Автор ответа:
2
vladonischuk:
Спасибо
на кнопочку "спасибо" нажми
Похожие вопросы
Предмет: Обществознание,
автор: balzigitarsen
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: abdraimovarsen6
Предмет: История,
автор: Аноним