Предмет: Математика,
автор: vladonischuk
Упростить выражения :
Приложения:
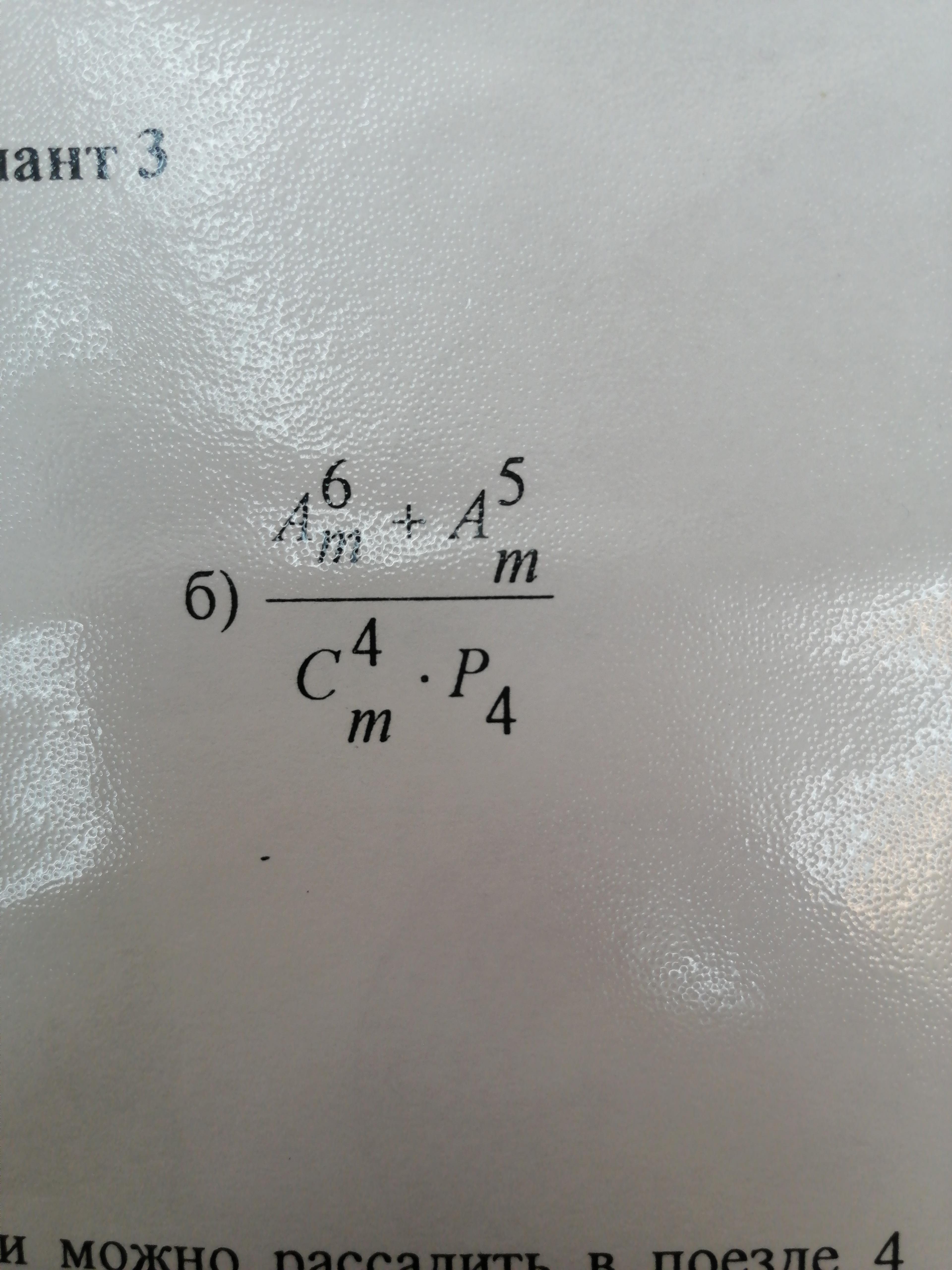
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Физика,
автор: kris2246
Предмет: Математика,
автор: mkirillova276
Предмет: Математика,
автор: PARAVOZIKPIDORAS1231
Предмет: История,
автор: Алёнчик200330