Предмет: Геометрия,
автор: hducudegg67
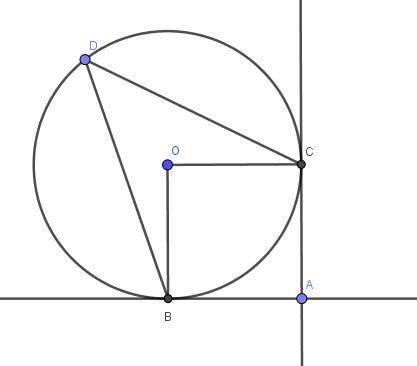
из точки А к окружности радиуса 7 см проведены касательные АВ и АС (В и С точки касания). точка D принадлежит большей из дуг ВС. найдите угол ВDС, если АВ равна 7 см.
Ответы
Автор ответа:
4
AB = AC = 7 см как касательные к окружности, BO = OC = 7 см как радиусы. Радиусы, проведенные в точку касания окружности, перпендикулярны касательным, а так как стороны четырехугольники ABCD равны и ∠OCA = ∠OBA = 90°, то ABCD - квадрат.
∠BOC - центральный угол, тогда вписанный угол BDC равен половине центрального угла, т.е. ∠BDC = ∠BOC/2 = 90°/2 = 45°
Ответ: 45°
Приложения:
Похожие вопросы
Предмет: Физика,
автор: lejlaajvazova517
Предмет: Физика,
автор: Аноним
Предмет: Геометрия,
автор: anonimus01844
Предмет: Математика,
автор: ппппррррооо
Предмет: Литература,
автор: aelita200507