Предмет: Математика,
автор: nashida97
Вычислить производную методом логарифмического дифференцирования 1) y=(x^2+3)^2x+4
Приложения:

nashida97:
2 пример,если что,тоже непонятен и вызывает бурю непонимания решения
свойства логарифмов надо знать, тогда всё понятно будет
Ответы
Автор ответа:
0
Ответ:
Решение на фото
.
.
.
.
.
.
.
.
Приложения:
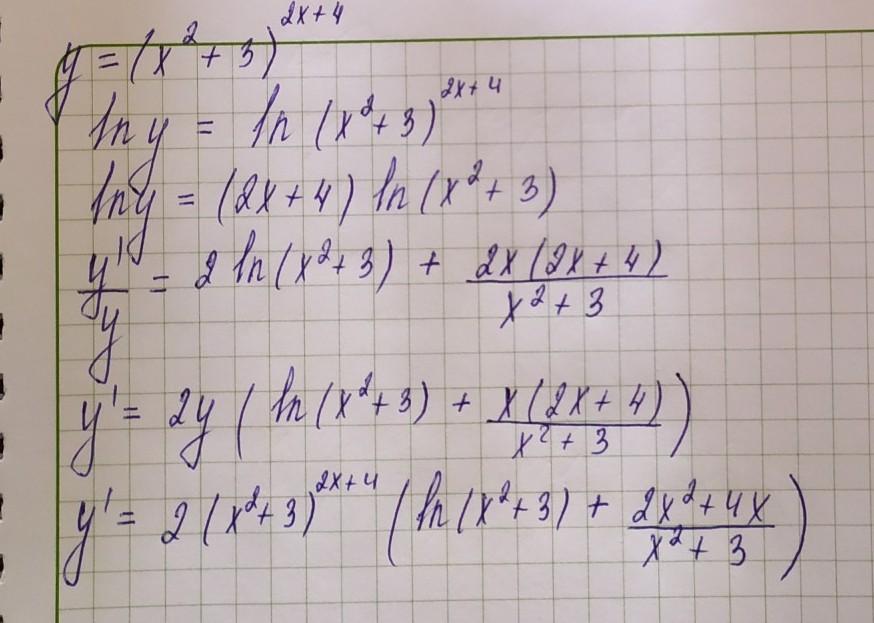
потеряли "2" в 5 строчке в числителе
Автор ответа:
0
Похожие вопросы
Предмет: Биология,
автор: ilya09022010
Предмет: Английский язык,
автор: kaliyeva0421
Предмет: Українська література,
автор: gopka37
Предмет: Математика,
автор: Аноним