Предмет: Алгебра,
автор: kskate452633
Найдите найбольшее значение выражения
Приложения:
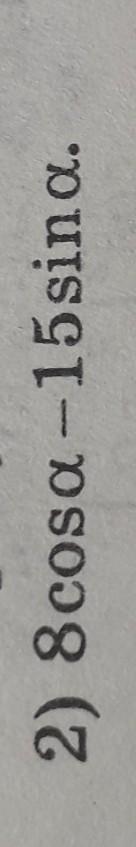
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Алгебра,
автор: problet53
Предмет: Геометрия,
автор: vladpatskal2
Предмет: Математика,
автор: oilabuvbomko
Предмет: Математика,
автор: мудрец19
Предмет: Алгебра,
автор: pryanex