Предмет: Алгебра,
автор: Аноним
Докажите тождество. (Срочно! Решите все, пожалуйста)
Приложения:
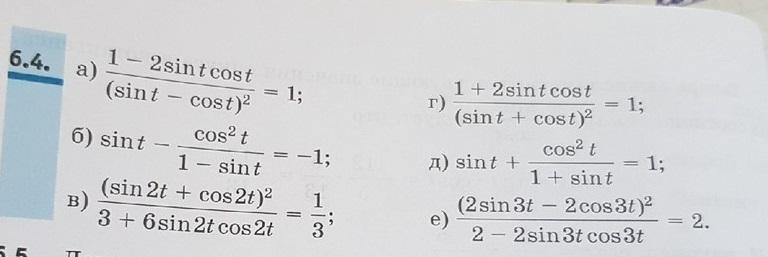
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Геометрия,
автор: 34nst
Предмет: Математика,
автор: emptiness177
Предмет: Математика,
автор: kharkovalera2011
Предмет: Литература,
автор: кристинкаverskova290
Предмет: Литература,
автор: Пушистик765783