Предмет: Геометрия,
автор: Никита256366
площадь трапеции abcd равна 162 а длины ее оснований равны ad 28 bc 8 найдите площадь треугольника AOD, где точка О пересечение диагоналей AC и BD
Ответы
Автор ответа:
9
Ответ:
98 кв. ед.
Объяснение:
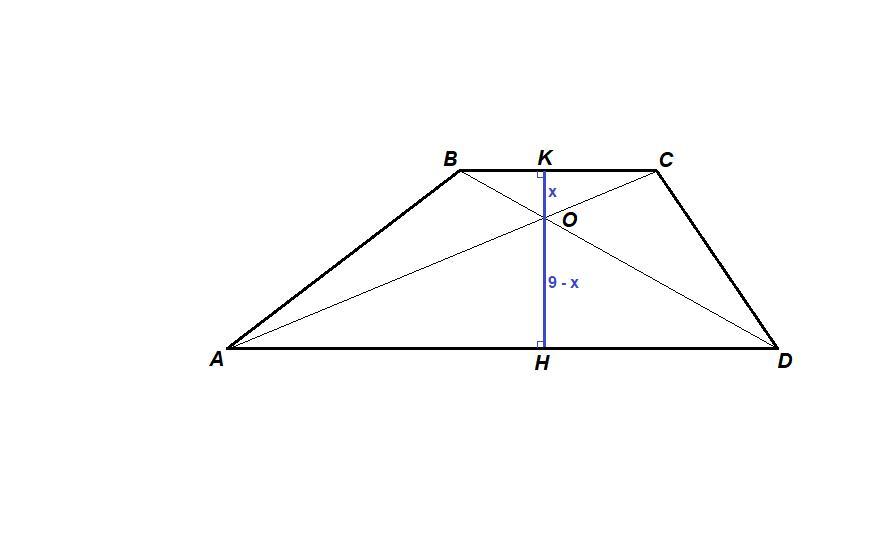
Проведем высоту КН через точку пересечения диагоналей.
Площадь трапеции:
ΔAOD ~ ΔCOB по двум углам (∠OAD = ∠OCB как накрест лежащие при пересечении параллельных прямых AD и ВС секущей АС, углы при вершине О равны как вертикальные).
Отношение высот подобных треугольников, проведенных к сходственным сторонам, равно отношению этих сторон:
Пусть ОК = х, тогда ОН = КН - х = 9 - х.
28x = 8(9 - x)
28x = 72 - 8x
36x = 72
x = 2
OK = 2, ⇒ OH = 9 - 2 = 7
Площадь ΔAOD:
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: jannurkuanyshova
Предмет: Українська мова,
автор: kostenkogleb438
Предмет: ОБЖ,
автор: lena3300
Предмет: Литература,
автор: Osipovaleria