Предмет: Алгебра,
автор: Aswacon
Помогите пожалуйста, очень надо
Приложения:
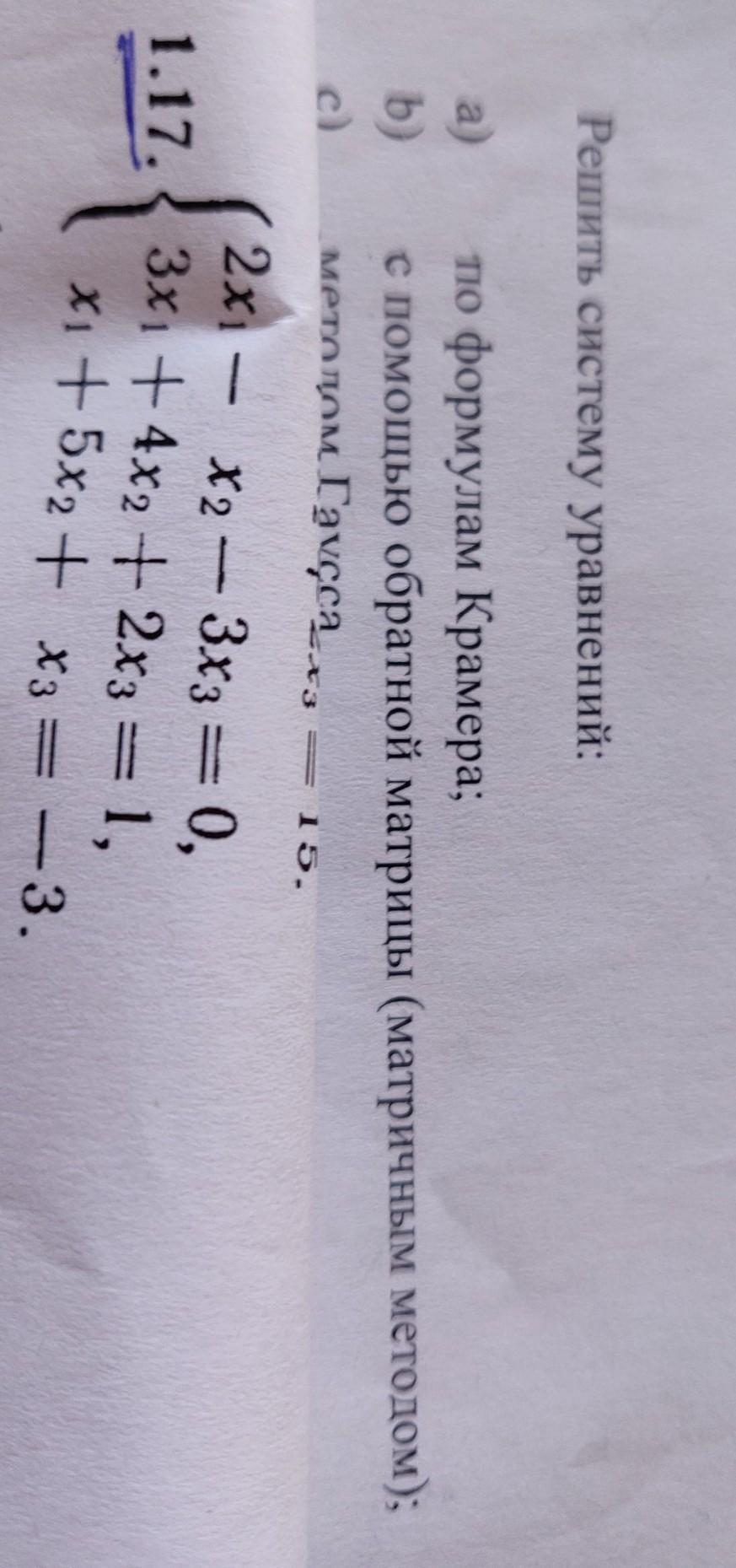
Ответы
Автор ответа:
1
1) Правило Крамера.
2) С помощью нахождения обратной матрицы.
3) Метод Гаусса.
Похожие вопросы
Предмет: Математика,
автор: rusiaketi
Предмет: Геометрия,
автор: pro008616
Предмет: Математика,
автор: Sanzhardavletov2011
Предмет: Математика,
автор: ник2903
Предмет: География,
автор: Янго5002