Предмет: Алгебра,
автор: Hunta123
Доказать, что (см. вложение)
Приложения:
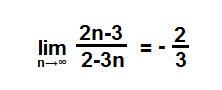
Simba2017:
что тут доказывать, это просто этот предел равен такой дроби
А почему именно этой, а не какой либо другой?
надо разделить и числитель и знаменатель на n
в числителе будет 2-3/n
3/n стремится к 0. значит числитель к 2
в знаменателе при делении на n будет
2/n-3
2/n стремится к 0, значит знаменатель стремится к -3
поэтому вся дробь стремится к -2/3
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Автор ответа:
0
Похожие вопросы
Предмет: Українська мова,
автор: dentkachuk2010
Предмет: География,
автор: tatesa
Предмет: Математика,
автор: Bulk121
Предмет: Математика,
автор: РоминаБ
Предмет: История,
автор: LizazaGreen