Question

Через точку A проведена касательная AB к окружности с радиусом 3(B-точка касания), отрезок BC - диаметр этой окружности. Найдите угол BAC, если AC=6корень из 2

​

Answer 1

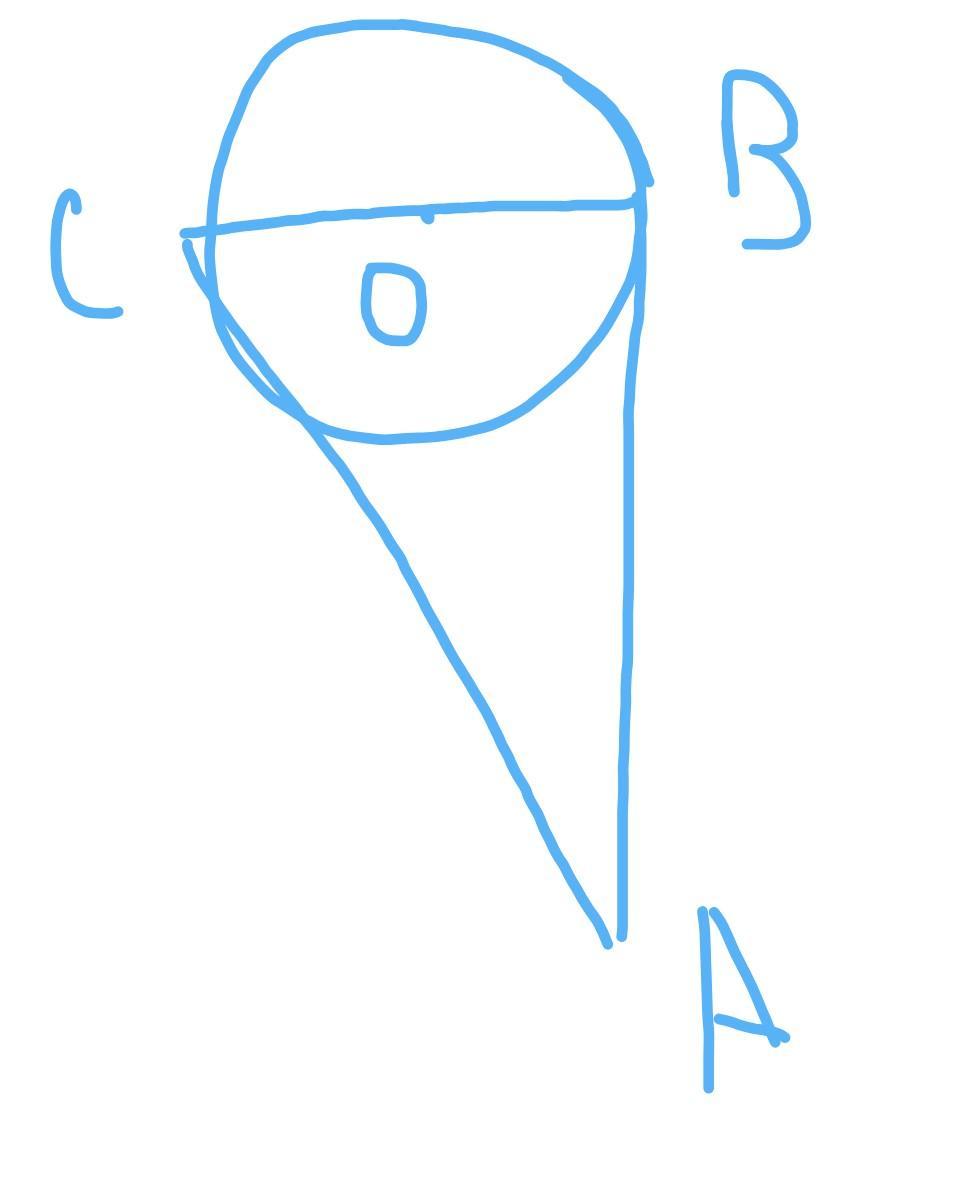
Схематический рисунок приложен.

АВ - касательная - значит она с ОВ и ВС образовывает угол 90° (касательная перпендикулярна к радиусу)

Следовательно, мы имеет прямоугольный треугольник АВС, угол В=90°

СВ=2R = 6 (не знаю чего, может сантиметров)

Отношение противоположного катета ВС к гипотенузе АС равно синус угла В

$\sin(A) = \frac{BC}{AC} = \frac{6}{6 \sqrt{2} } = \frac{1}{ \sqrt{2} } = \frac{ \sqrt{2} }{2} \\ \\ A= 45°$

Ответ: 45°

Answer 2

решение и ответ во вложении