Предмет: Алгебра,
автор: Natka1223
Вычислить(комплексное число):
(1+i^5)^2(1-4i)-((1-i)/(1+i))
Ответы
Автор ответа:
1
Автор ответа:
1
Решение и ответ во вложении
Приложения:
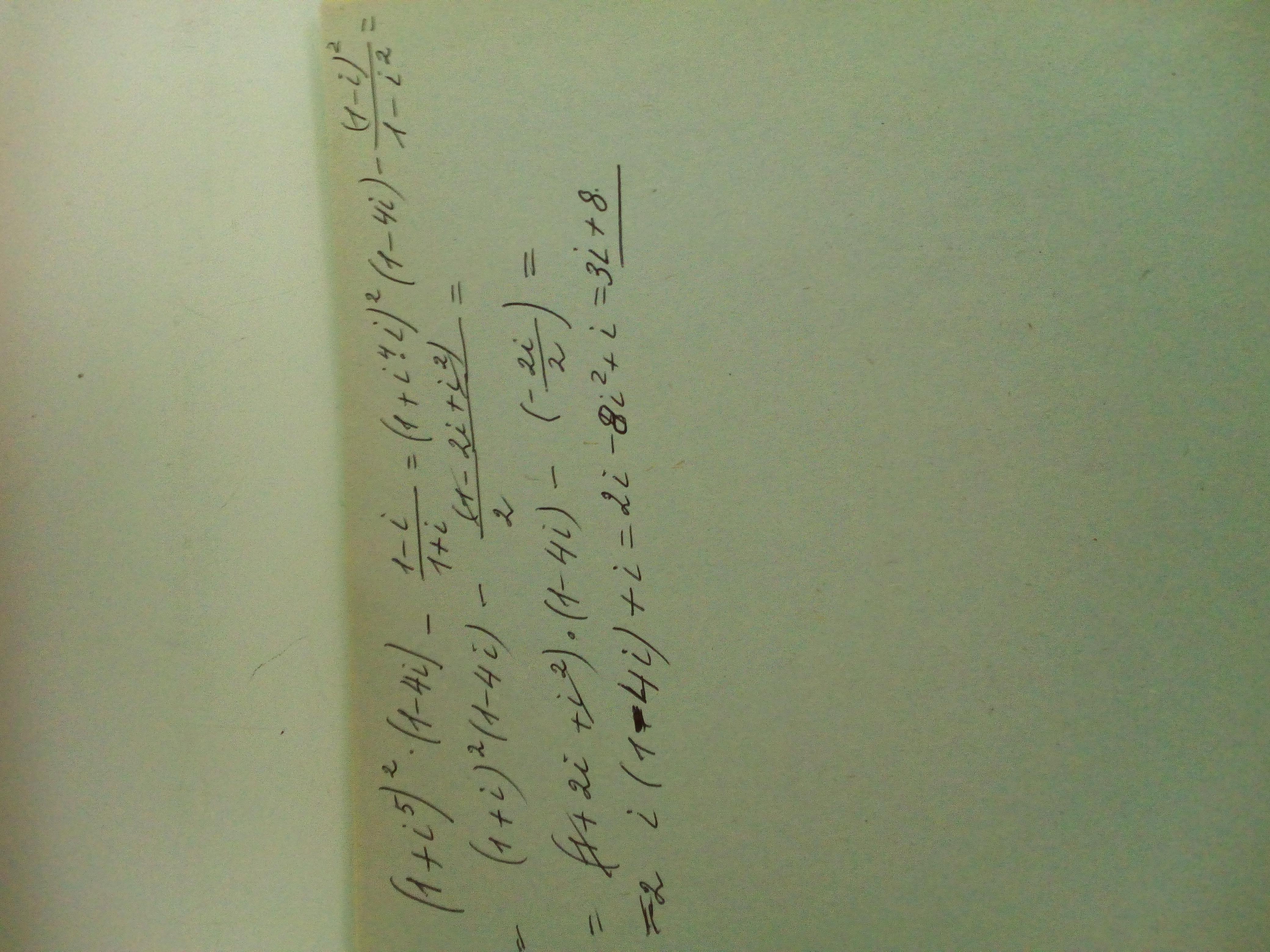
Похожие вопросы
Предмет: Алгебра,
автор: loskarevan80
Предмет: Математика,
автор: evgeniasav
Предмет: Математика,
автор: xilalovay
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Лера156432