Question

В лесу расположились три охотника. Каждый охотник контролирует участок в форме круга с центром в точке его расположения и некоторым радиусом. Определите, какова наибольшая суммарная площадь контролируемой охотниками территории, если участки охотников не могут пересекаться (но могут касаться друг друга), если известны координаты охотников.

Гарантируется, что все три охотника не находятся на одной прямой.

Ответ вывести как десятичную дробь, с точностью до 4 знаков после запятой.

x1 = 4, y1 = 9.

x2 = 5, y2 = 1.

x3 = 12, y3 = 7.

Answer 1

Ответ:

Максимально возможная суммарная площадь обзора

Sобщ.=216.6046 ед.²

Пошаговое объяснение:

Поскольку в задании чётко не ограничен минимальный радиус обзора охотников, то примем его за 0 (охотник уснул).

Площадь обзора каждого из охотников представляет собой круг.

Формула площади круга:

S=πR².

Как видно из формулы площади круга, зависимость от радиуса обзора - квадратичная. Это говорит о том, что для получения максимальной площади обзора, лучше получить один максимально большой круг и два оставшихся небольших, чем два одинаковых и один поменьше или три примерно одинаковых круга. Справедливость этого утверждения подтверждает форма графика квадратичной параболы, и понимание того, что при суммировании площадей мы выполняем "линейную" операцию.

Для того, чтобы определить максимальный круг обзора, нам нужно вычислить расстояния между точками, в которых расположены охотники. Для удобства обозначим точки буквами А(4;9), В(5;1); С(12;7).

Найдем АВ: $\sqrt{(5-4)^{2}+(1-9)^{2}} =\sqrt{65} =8,0623$

Найдем АС: $\sqrt{(12-4)^{2}+(7-9)^{2}} =\sqrt{68} =8,2462$

Найдем ВС: $\sqrt{(12-5)^{2}+(7-1)^{2}} =\sqrt{85} =9,2195$

Значит "отдаем приоритет" охотнику в точке С, т.к. два самых длинных расстояния АС и ВС связаны с этой точкой. Охотника в точке А - "усыпляем", т.е. даём ему радиус обзора,  равный 0, при этом он вырождается в точку с площадью, равной нулю.

Радиус обзора охотника в точке С принимаем равным АС, иначе если его принять бОльшим, то в площадь обзора включится точка А, что равносильно пересечению участков охотников.

Тогда получаем три площади обзора с радиусами:

0;  АС; (ВС-АС)

Вычислим эти площади.

Для точки А: Sa=0 ед.²

Для точки С: Sc=π*АС²=213,6283 ед.²

Для точки В: Sb=π*(BC-АС)²=2.9763 ед.²

Sобщ.=0+213,6283+2,9763=216.6046 ед.²

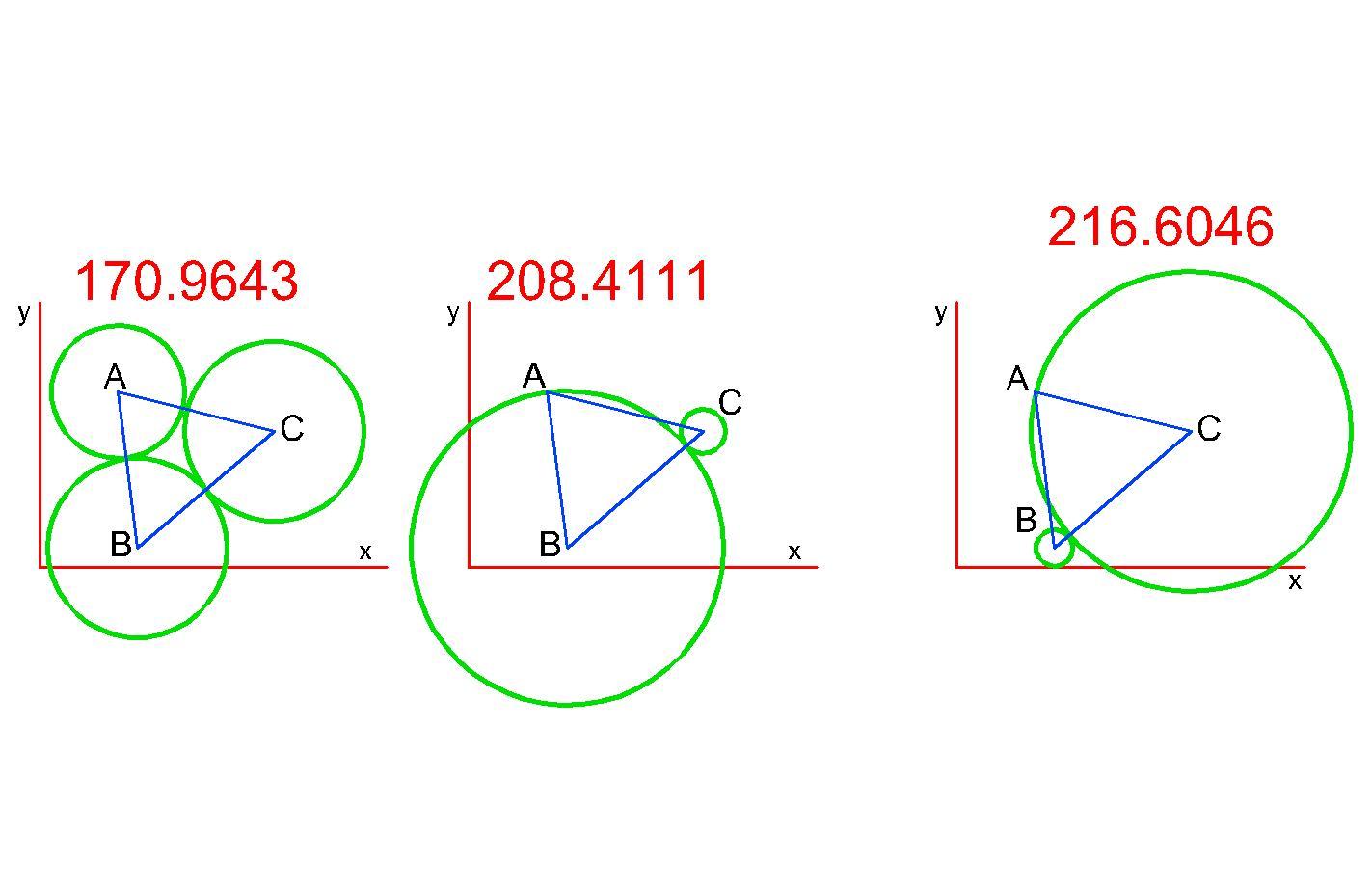
На рисунке прилагаю 3 возможных варианта обзоров охотников из которых только последний (крайний справа) - правильный.