Предмет: Алгебра,
автор: mashachanmasha
помогиие пожалуйста
Приложения:
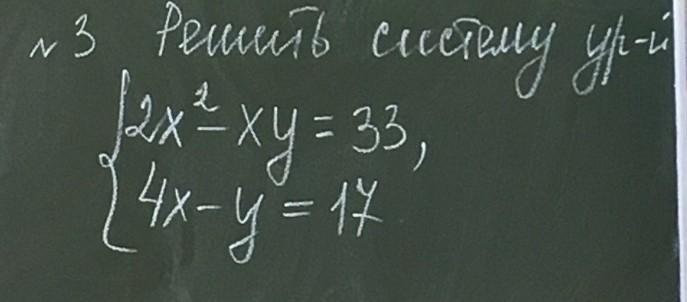
mashachanmasha:
помогите"
Ответы
Автор ответа:
1
Автор ответа:
4
Похожие вопросы
Предмет: История,
автор: valeriya8599
Предмет: Математика,
автор: juliabondarenko2511
Предмет: Биология,
автор: Riokrash
Предмет: Математика,
автор: SaChA235
Предмет: История,
автор: Moonstoun