Предмет: Алгебра,
автор: panda15052003
Помогите решить уравнение
Приложения:
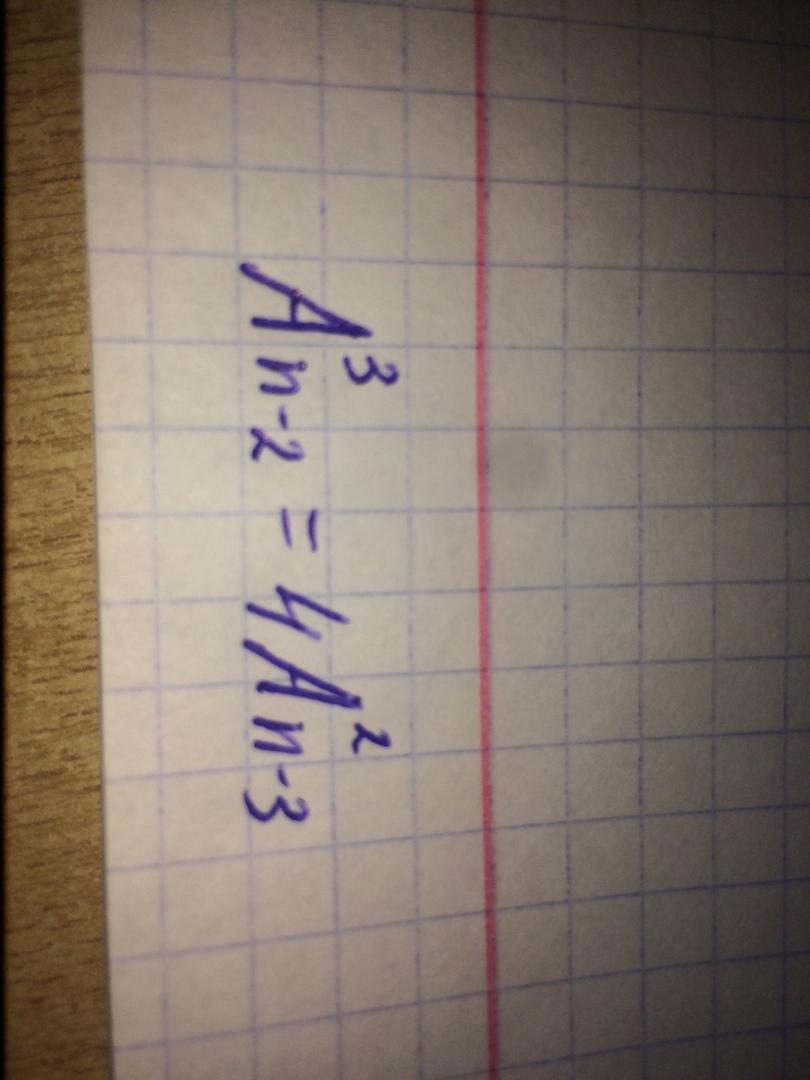
Ответы
Автор ответа:
2
Число размещений равно (n-2)(n-3)(n-4)=4*(n-3)(n-4)
(n-2)(n-3)(n-4)-4*(n-3)(n-4)=0
(n-3)(n-4)(n-2-4)=0
n-3=0⇒n=3
n-4=0⇒n=4
n-2-4=0⇒n=6
Подходит только 6.
Аноним:
Проверьте решение.
Хотя у себя сейчас посмотрю что не так
А всё, у меня ошибка...
Автор ответа:
1
Число размещений:
n = 4 и n = 3 отбрасываем
Ответ: 6.
Решение исправил
Мне кажется, что 3 и 4 не подходят.
Вы, правы
Похожие вопросы
Предмет: Математика,
автор: karpenko201027
Предмет: Немецкий язык,
автор: orestdunko2010
Предмет: Английский язык,
автор: valeriasheremet10
Предмет: Биология,
автор: Аноним