Предмет: Математика,
автор: Громова203
Найти производные .....
Приложения:
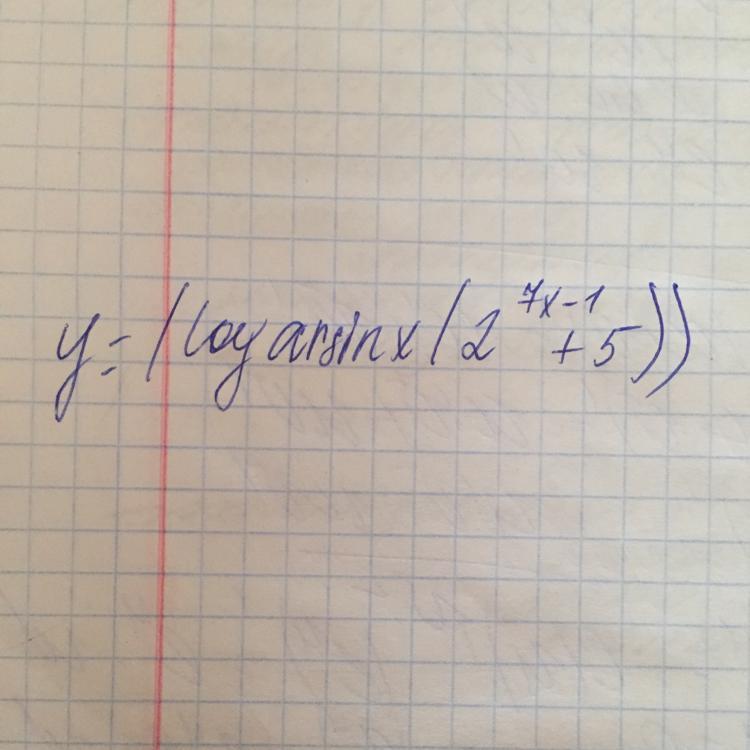
NNNLLL54:
log по какому основанию ?
там х как основание идет
a "arcsinx" - это множитель ?
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Геометрия,
автор: kubovaaliona
Предмет: Биология,
автор: dimanzuk12
Предмет: Геометрия,
автор: nastyapapazova36
Предмет: Математика,
автор: Кристина20052016
Предмет: Математика,
автор: еа06544еа