Предмет: Алгебра,
автор: hhvc39
Решить способом подставки
Приложения:
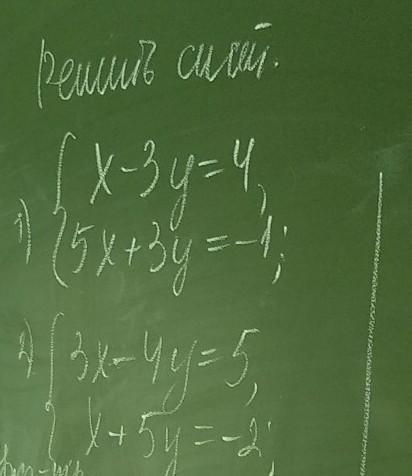
Ответы
Автор ответа:
2
Автор ответа:
0
Похожие вопросы
Предмет: Геометрия,
автор: mariaokopnaa296
Предмет: Английский язык,
автор: innashypovskih
Предмет: Математика,
автор: livinets50
Предмет: Математика,
автор: cuzmins460
Предмет: Математика,
автор: Диана101005