И еще поясните как решать такие задачи.
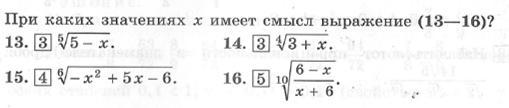
Ответы
1) Выражения под корнем нечётной степени могут принимать любые значения, как положительные, так и отрицательные и ноль.
2) Выражения под корнем чётной степени могут принимать неотрицательные (положительные и ноль) значения.
Выражение 13 имеет смысл при любых действительных числах, поскольку корень нечетной степени извлекается из любого числа.
14.При х∈[-3;+∞), в этом случае подкоренное выражение неотрицательно.
15. -х²+5х-6=-(х²-5х+6) ≥0, (х²-5х+6)≤0, (х-2)(х-3)≤0 решим методом интервалов.
__________2_______3______
+ - +
х∈[2;3]
16. дробь существует, когда она неотрицательна, т.е.
(6-х)/(х+6)≥0, а это возможно, когда (6-х)*(х+6)≥0 и х≠-6 методом интервалов находим ответ
______-6______6___
- + -
х∈(-6;6]