Question

Сторона основания правильной треугольной призмы равна 6, высота призмы корень из 13. Через центр нижнего основания и ребро A1B1 Верхнего основания проведена плоскость. Найдите площадь сечения призмы данной плоскостью.

Answer 1

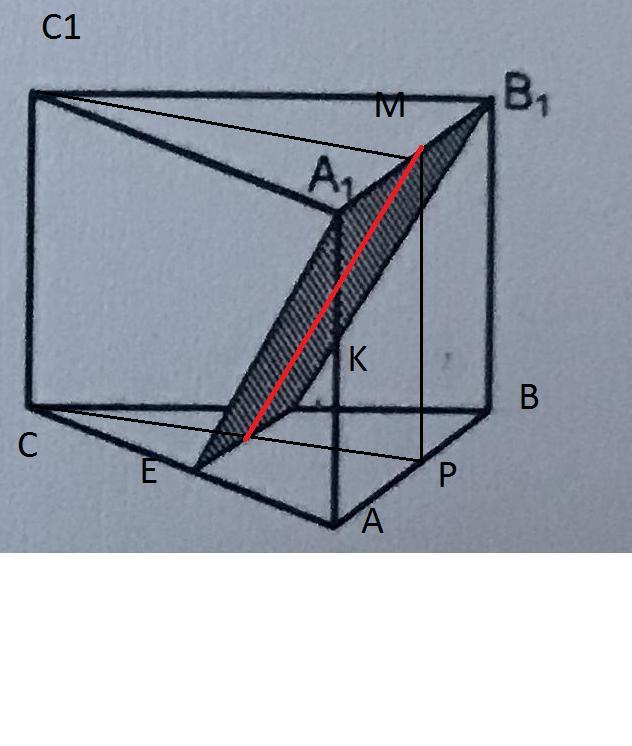
Если плоскость сечения проведена через А1В1, то линия ЕК сечения основания АВС параллельна А1В1.

Пусть точка О - центр основания АВС.

Высота СР проходит через точку О и делится ею  в отношении СО/ОР = 2/3. Также из условия подобия ЕК = (2/3)АВ = (2/3)*6 = 4.

Отрезок ОР = (1/3)СР = (1/3)*6*(√3/2) = √3.

В сечении имеем равнобокую трапецию ЕА1В1К.

Находим её высоту OМ = √(ОР² + РМ²) = √(3 + 13) = √16 = 4.

Получаем ответ: S = EK*OM = 4*4 = 16 кв.ед.