Question

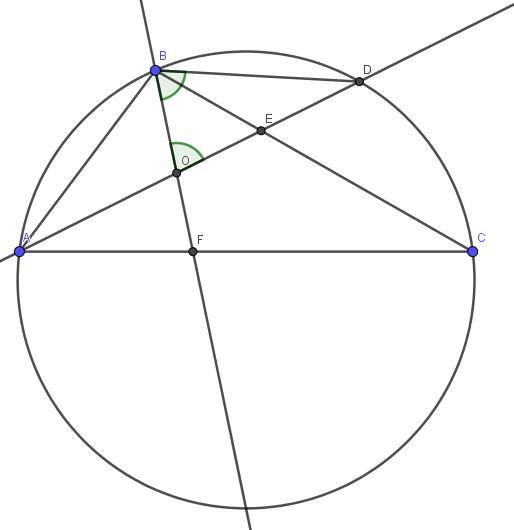
Биссектриса угла А треугольника АВС пересекает биссектрису угла В в точке О, а окружность, описанную около треугольника, в точке D. Докажите, что угол BOD = углу OBD

Answer 1

$AE$ - биссектриса угла $BAC$, следовательно, $\angle BAE=\angle EAC$.

$BF$ - биссектриса угла $ABC$, следовательно, $\angle ABF=\angle FBC$

Рассмотрим треугольник $AOB:$ сумма углов треугольника равна 180°, т.е.

$\angle ABO+\angle AOB+\angle BAO=180^\circ\\ \\ 180^\circ-\angle AOB=\angle ABO+\angle AOB$

$\angle BOD$ - внешний угол треугольника $AOB$ при вершине B, значит $\angle BOD=\angle ABO+\angle BAO$

$\angle OBD=\angle OBE + \angle EBD$, но $\angle ABO=\angle OBE$ и $\angle CBD=\angle DAC$ (углы опирающиеся на одну и ту же дугу равны) откуда $\angle CBD=\angle BAD~\Rightarrow~ \angle EBD=\angle BAO$

Следовательно, $\angle OBD=\angle ABO+\angle BAO$ отсюда и следует равенство углов $OBD$ и $BOD$

Что и требовалось доказать.