Предмет: Математика,
автор: kotovaaa78
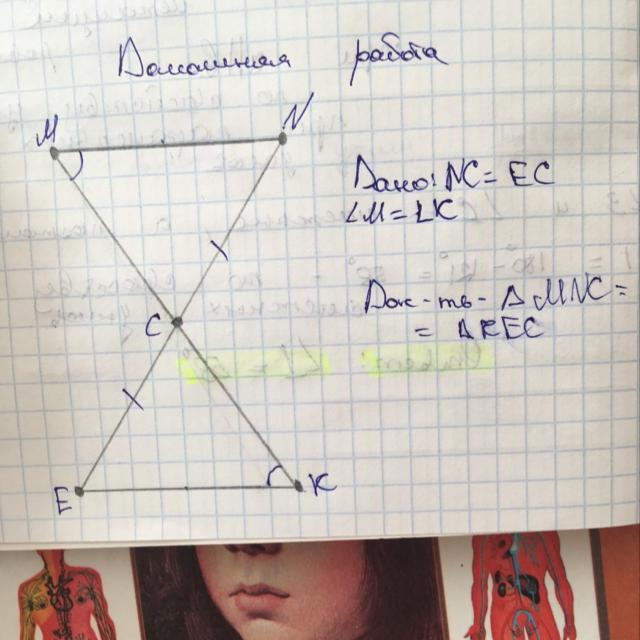
Дано: треугольник MNC и треугольник KEC, NC=EC,угол M=углу K
Приложения:
Ответы
Автор ответа:
2
Поскольку накрест лежащие углы равны: , то по первому признаку параллельности прямых, прямые
как накрест лежащие углы при
и секущей
как вертикальные и по условию
, следовательно,
по стороне и двум прилежащим к ней углам.
Что и требовалось доказать.
Похожие вопросы
Предмет: Геометрия,
автор: kirasmith0918
Предмет: Литература,
автор: Аноним
Предмет: Химия,
автор: evgeshalovegordeeva
Предмет: Математика,
автор: Natalya3627
Предмет: Алгебра,
автор: maghomiedov2002